☖ Home ⇄ Units Converter ⧉ Geometry Σ Math ✈ Physics 〶 Electricity

Two lines intersection calculator

Print two lines intersection calculator
Line 1 Equation
 
 x 
+
 
 y 
+
 
 = 0
2 points
(x1,y1) (
 
)
(x2,y2) (
 
)
Slope, Point
(xp,yp) ( ) Angle = Slope =
Line 2 Equation
 
 x 
+
 
 y 
+
 
 = 0
2 points
(x1,y1) (
 
)
(x2,y2) (
 
)
Slope, Point
(xp,yp) ( ) Angle = Slope =
Lines equations 1,2
Angle between lines
Intersection point (x,y)
Angle
Bisector
lines		 Equations
Slopes
Angles
Degree
Radian

Two lines intersection summary

Print two lines intersection summary
y = m1x + a
y = m2x + b
Where in vector notation:
A = m1i - j
B = m2i − j
The intersection point is determined by solving the values of x and y from the two lines equations by Cramer's rule or by direct substitution:
If     m2 − m1 = 0     then both lines are parallel.
The angle between two lines in the range   0 < θ < π/2   is:
Angle between two lines
The angle between the two lines can be calculated by vector dot product method:       A · B = |A| |B|cos θ
Note: the ± sign stands for the two possible angles between two lines that are complementary to  180 degrees.
If the two lines are given by the equations:
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
The intersection point is determined by solving the values of x and y from the two lines equations:
If     a1b2 − a2b1 = 0     then both lines are parallel.
If both lines are each given by two points, first line points:     (x1 , y1) , (x2 , y2) and the second line is given by two points:
(x3 , y3) , (x4 , y4)
The intersection point (x , y) is found by the equations: (see example)
Example: find the intersection point and the angle between the lines:
x − 2y + 3 = 0
3x + 4y + 1 = 0
Solving the lines equations for x and y by Cramer's rule.
And the intersection point is at (− 1.4 , 0.8)
The angle between the lines is:
If the two solutions are added, then:   63.43 + 116.57 = 180   as we expected.

Two lines angle bisector summary

Print two lines angle bisector summary
If the lines are given by the equations:
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
The distance (d) of any common point (x , y) which lies on the angle bisector from the two given lines are the same (two similar triangles).
distance of point (x , y) from line (1)
distance of point (x , y) from line (2)
And the equations of the (acute and the other is obused) angle bisector lines are:
After some manipulations we recieve the bisector line equation:

(a_1-a_2 φ)x+(b_1-b_2 φ)y+c_1-c_2 φ=0

Where: φ=√((〖a_1〗^2+〖b_1〗^2)/(〖a_2〗^2+〖b_2〗^2 ))
Note: The Plus and minus sign is used to find the two possible angle bisectors lines equation which are  90  degrees apart.
If the lines are given by the equations:
y = m1x + a
y = m2x + b

Distance from a point on the bisector to the line:

d=|m_1 x+y+a|/√(〖m_1〗^2+1)=|m_2 x+y+b|/√(〖m_2〗^2+1)

The equation of the angle bisector will be:

(m_1-m_2 φ)x+(1-φ)y+a-φb=0

Where:
φ=√((〖m_1〗^2+1)/(〖m_2〗^2+1))
Lines given by the equations:
y = m1x + a
y = m2x + b
The angle of the lines angle bisector from the x axis is:
The equation of the angle bisector line is:
First line:
A second angle bisector exists at a right angle from the first line.
Second line:
Where:
mb can be expressed by the slopes m1 and m2 of the lines as:
The ± sign stands for the two angle bisectors possible between two lines (complementary to 180 degree).
Angle bisector line equation expressed by m1 and m2 is:
y − y0 = mb(x − x0)

Example 1 − Intersection of 2 lines each defined by 2 points

Print two lines intersection example
Find the intersection point of two lines each of them defined by two pair of coordinates, first line by
(x1 y1) (x2 y2) and second line by (x3 y3) and (x4 y4).

The equations of two arbitrary lines are:    y = m1 x + a  and       y = m2 x + b

This equation can be easily solved by comparing the y values of both equations:   m1 x + a = m2 x + b

And the solutions are:
x=(a-b)/(m_2-m_1 )
and
y=(m_1 (a-b))/(m_2-m_1 )+a
Line slope
from the sketch the slope  m1  is:
m_1=tan⁡θ=(y_2-y_1)/(x_2-x_1 )
the solution for slope  m2  is:
m_1=tan⁡θ=(y_2-y_1)/(x_2-x_1 )
The slope m1 can be written as a function of x and y as:
m_1=(y-y_1)/(x-x_1 )
or
m_1 (x-x_1 )=y-y_1
And the line equation will be:
y=m_1 x+(y_1-m_1 x_1 )
We can see that the free item that is  a  in the line equation is equal to  a = y1 − m1x1  and for the second line  b = y3 − m2x3

Now that we have found all the values of m1 m2 a  and  b,  we can substitute those values to the  x  and  y  coordinate of the intersection point.
x=(a-b)/(m_2-m_1 )=(y_1-(y_2-y_1)/(x_2-x_1 ) x_1-y_3+(y_4-y_3)/(x_4-x_3 ) x_3)/((y_4-y_3)/(x_4-x_3 )-(y_2-y_1)/(x_2-x_1 ))
=(((x_2-x_1 )(x_4-x_3 )(y_1-y_3 )-(x_4-x_3 )(x_1 y_2-x_1 y_1 )+(x_2-x_1 )(x_3 y_4-x_3 y_3 ))/(x_2-x_1 )(x_4-x_3 ) )/(((x_2-x_1 )(y_4-y_3 )-(x_4-x_3 )(y_2-y_1 ))/(x_2-x_1 )(x_4-x_3 ) )
=((x_2-x_1 )(x_4-x_3 )(y_1-y_3 )-(x_4-x_3 )(x_1 y_2-x_1 y_1 )+(x_2-x_1 )(x_3 y_4-x_3 y_3 ))/((x_2-x_1 )(y_4-y_3 )-(x_4-x_3 )(y_2-y_1 ) )
=(x_2 x_4 y_1-x_2 x_3 y_1-x_2 x_4 y_3+x_1 x_4 y_3-x_4 x_1 y_2+x_3 x_1 y_2+x_2 x_3 y_4-x_1 x_3 y_4)/((x_2-x_1 )(y_4-y_3 )-(x_4-x_3 )(y_2-y_1 ) )
=(x_2 y_1 (x_4-x_3 )-x_4 y_3 (x_2-x_1 )-x_1 y_2 (x_4-x_3 )-x_3 y_4 (x_2-x_1 ))/((x_2-x_1 )(y_4-y_3 )-(x_4-x_3 )(y_2-y_1 ) )
x=((x_2 y_1-x_1 y_2 )(x_4-x_3 )-(x_4 y_3-x_3 y_4 )(x_2-x_1 ))/((x_2-x_1 )(y_4-y_3 )-(x_4-x_3 )(y_2-y_1 ) )
And the same process accompanied with some basic algebra steps we get the y coordinate:
y=(m_1 (a-b))/(m_2-m_1 )+a=((y_2-y_1)/(x_2-x_1 ) (y_1-m_1 x_1-y_3+m_2 x_3 ))/((y_4-y_3)/(x_4-x_3 )-(y_2-y_1)/(x_2-x_1 ))+y_1-m_1 x_1
=(m_2 (y_1-m_1 x_1 )-m_1 (y_3-m_2 x_3 ))/(m_2-m_1 )=(m_2 y_1-m_1 m_2 x_1-m_1 y_3+m_1 m_2 x_3)/(m_2-m_1 )
=(m_1 m_2 (x_3-x_1 )+m_2 y_1-m_1 y_3)/(m_2-m_1 )
Now substitute the values of m1 and m2 to get:
=((y_2-y_1)/(x_2-x_1 ) (y_4-y_3)/(x_4-x_3 ) (x_3-x_1 )+(y_4-y_3)/(x_4-x_3 ) y_1-(y_2-y_1)/(x_2-x_1 ) y_3)/((y_4-y_3)/(x_4-x_3 )-(y_2-y_1)/(x_2-x_1 ))
=(((y_2-y_1 ))/((x_2-x_1 ) ) ((y_4-y_3 ))/((x_4-x_3 ) ) (x_3-x_1 )+(x_2-x_1 )(y_4-y_3 )/(x_2-x_1 )(x_4-x_3 ) y_1-(x_4-x_3 )(y_2-y_1 )/(x_4-x_3 )(x_2-x_1 ) y_3)/(((x_2-x_1 )(y_4-y_3 )-(x_4-x_3 )(y_2-y_1 ))/(x_2-x_1 )(x_4-x_3 ) )
=((y_2-y_1 )(y_4-y_3 )(x_3-x_1 )+(x_2 y_1-x_1 y_1 )(y_4-y_3 )-(x_4 y_3-x_3 y_3 )(y_2-y_1 ))/((x_2-x_1 )(y_4-y_3 )-(x_4-x_3 )(y_2-y_1 ) )
=(x_3 y_2 y_4-x_3 y_1 y_4-x_1 y_2 y_4+x_1 y_2 y_3+x_2 y_1 y_4-x_2 y_1 y_3-x_4 y_2 y_3+x_4 y_1 y_3)/((x_2-x_1 )(y_4-y_3 )-(x_4-x_3 )(y_2-y_1 ) )
=(y_4 (x_2 y_1-x_1 y_2 )-y_3 (x_2 y_1-x_1 y_2 )-y_2 (x_4 y_3+x_3 y_4 )+y_1 (x_4 y_3-x_3 y_4 ))/((x_2-x_1 )(y_4-y_3 )-(x_4-x_3 )(y_2-y_1 ) )
y=((x_2 y_1-x_1 y_2 )(y_4-y_3 )+(x_4 y_3+x_3 y_4 )(y_2-y_1 ))/((x_2-x_1 )(y_4-y_3 )-(x_4-x_3 )(y_2-y_1 ) )

Example 2 − Two lines angle bisector

Print two lines angle bisector example
Given two lines equations: 3x − 4y + 2 = 0 5x + 12y + 1 = 0
Find the angle between the lines and the equation of the angle bisector between the two lines.
The angle between the lines is found by vector dot product method.
We can write the lines general direction by vector notation as:
L1 = a1i + b1j       and       L2 = a2i + b2j
The dot product of these two vectors is related to the angle by the formula:       L1 · L2 = |L1||L2|cos θ
Where:
L1 · L2 = a1a2 + b1b2
Then the two possible angles are:
To find the angle bisector line equation, we use the distance equations:
And the two angle bisector lines equation are:
13(3x − 4y +2) = 5(5x + 12y + 1)
14x − 112y + 21 = 0
And the second line:
− 13(3x − 4y + 2) = 5(5x + 12y + 1)
64x + 8y + 31 = 0

Example 3 − Two lines angle bisector

Print example 3
Given two lines equations: L1:  x + 3y − 6 = 0     L2:  2x + y + 5 = 0
Find the angle between the lines and the equation of the acute angle bisector between the two lines.
The angle between the lines can be found by different ways, we will examine two methods.

Solution using the slopes:

Example 3

From the sketch we realize that:   α + β = π

Or we can write:   α = π − β

The slope of line L2 is   m2 = −2

Angle of line 2 is:

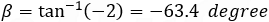
β=tan^(-1)⁡(-2)=-63.4 degree

We get a negative angle hence the angle is measured bellow the horizontal x axis (in our case the angle is β)

If we want the total positive angle from the x axis to the line (this is angle α) we must use the formula

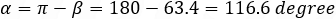
α=π-β=180-63.4=116.6 degree

of course, both values are valid because:

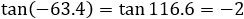
tan⁡〖(-63.4)=tan⁡〖116.6=-2〗

The same way we find the angles to line L1:

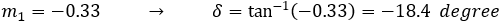
m_1=-0.33 → δ=tan^(-1)⁡(-0.33)=-18.4 degree

And the positive obtuse angle is:
γ=π-δ=180-18.4=161.6 degree

From the two lines slopes we can calculate the angles between the lines:

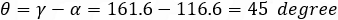
θ=γ-α=161.6-116.6=45 degree

The slope of the acute angle bisector is:   45 / 2 = 22.5 degree

The positive angle bisector of the lines is:   116.6 + 22.5 = 139.1 degree     (corresponding to −40.9 degree).

δ-θ/2=-18.4-22.5=40.9 degree

Next step is to find the intersection point of the given lines to get:     x = −4.2   and   y = 3.4

And the line equation of the angle bisector according to slope and a point is:

y = mbx +(y − mbx)

y = −0.866x − 0.24

Solution using vectors:

We will calculate the angle between the lines by changing the lines to vectors:

Vector presentation

The intersection coordinates as we found earlier is M: (−4.2 , 3.4)

Now we find two arbitrary points on both lines by substituting a chosen value of y = 6:

The points will be: on line L1: (−12 , 6) and on line L2: (−5.5 , 6)

The vectors of the lines can be found by the equation: V = (Mx − Lx)i + (My − Ly)j

VL1 = (−4.2 + 12)i + (3.4 − 6)j = 7.8i − 2.6j

VL2 = (−4.2 + 5.5)i + (3.4 − 6)j = 1.3i − 2.6j

The angle between the lines is:

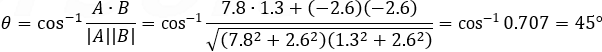
θ=cos^(-1)⁡〖(A∙B)/|A||B| 〗=cos^(-1)⁡〖(7.8∙1.3+(-2.6)(-2.6))/√((〖7.8〗^2+〖2.6〗^2 )(〖1.3〗^2+〖2.6〗^2 ) )〗=cos^(-1)⁡0.707=45°