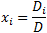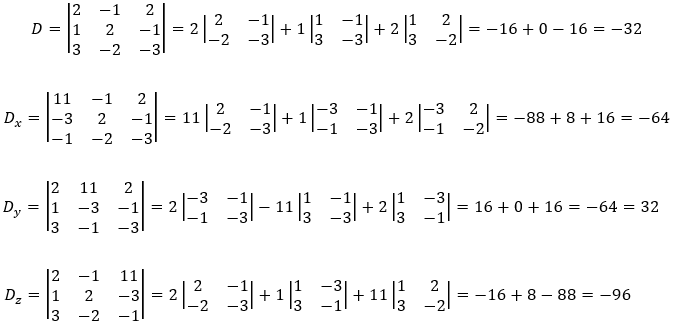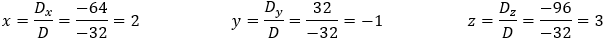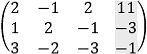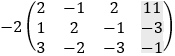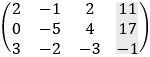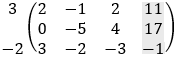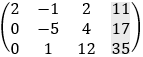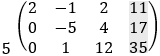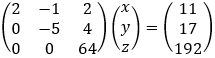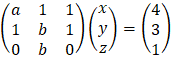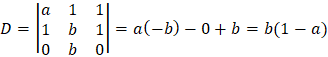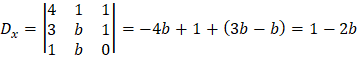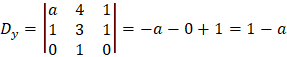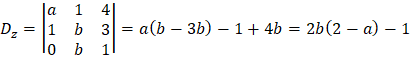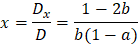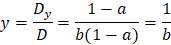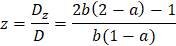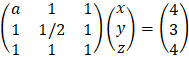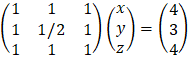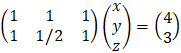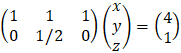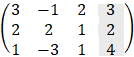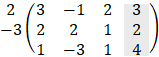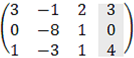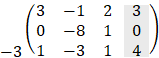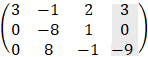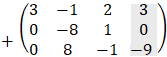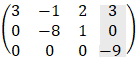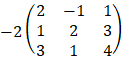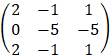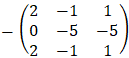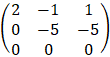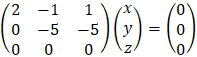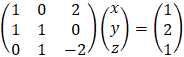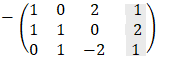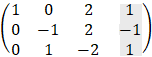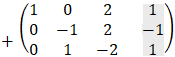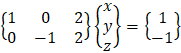Linear equations solver

System of Linear Equations Solver



Matrices eigenvalues and rotation matrix.

Solutions of the linear system of equations

x =

y =

z =

u =

v =

w =

r =

s =

t =

Cramer's rule Ex1 Ex2 Ex3 Ex4 Ex5 Ex6

System of linear equations

A system of m linear equations in n unknowns has a solution if and only if the rank r of the augmented matrix equals that of the coefficient matrix.
If the two matrices have the same rank r and r = n, the solution is unique.
If the two matrices have the same rank r and r < n, then at least one set of r of the unknowns can be solved in terms of the remaining (n − r) unknowns.

The general form of a linear system of equations can be presented by the formula: A x_i = B_i
Coefficient matrix	is the matrix which contains the variables coefficients (A matrix in the formula).
Constant matrix	is the array of the free column values (B_i vector array).
Augmented matrix	is the combined matrix which contains the Coefficient matrix and Constant matrix side by side (AB_i matrix).

Cramer's rule

Another way to solve linear system of equation is by Cramer's rule which involves only determinants. Consider the system of equations: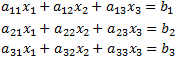

The solution is given by the equation:

D_i	− is the determinant established by changing the i column with the free values column b_i
D	− is the determinant of the Coefficient matrix.

Examples of solving linear system of equations

Example: Solve the system of linear equations of three variables x, y and z:

x − y + 2z = − 2

3x − 2y + 4z = − 5

2y − 3z = 2

Consider the system of linear equations containing three variables x, y and z. this equations cab be written in matrix notation as: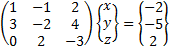

One way to solve the equations is by row transformation on the augmented matrix.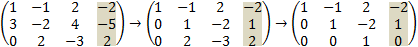

From the third line it is obvious that z = 0

From second line: y − 2z = 1 → y = 1

From first row: x − y + 2z = − 2 → x = − 1

Solving the above equations by Cramer' s rule.

Solve the above equations by Cramer' s rule.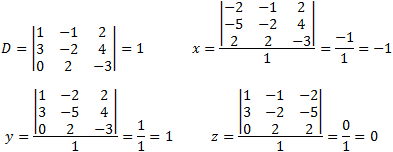

Example: Solve the system of the linear equations:

x + 2y − 3z = 4

x + 3y + z = 11

2x + 5y − 4z = 13

2x + 6y + 2z = 22

After performing rows operations, we get the upper triangular matrix:

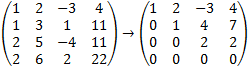It is seen that r = n (rank = number of variables) therefore the equations have a unique solution: z = 1 y = 3 x = 1 or in vector representation (1, 3, 1)

Example: Solve the system of the linear equations:

x + 2y − 2z + 3w = 2

2x + 4y − 3z + 4w = 5

5x + 10y − 8z + 11w = 12

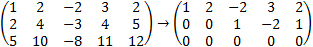The result is that r < n (r = 2 n = 4)

r − Rank of the matrix − total non zero rows

n − Number of variables

Because r − n = 4 − 2 = 2 two variables are dependent on the other two variables and we have to choose certain values for two variables
for example: w = a and y = b (a, b are any number) then:

z = 1 + 2a

x = 4 − 2b + a

The solution space vector is (4 + a − 2b, b, 1 + 2a, a)
for example if we choose: a = 1 b = − 1 then the solution is:
(7, − 1, 3, 1).

Example: Solve the system of the linear equations:

2x + y − 2z + 3w = 1

3x + 2y − z + 2w = 4

3x + 3y + 3z − 3w = 5

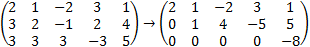From the last row it is observed that: 0 = 8 certainly, this is not possible, hence this set of equations don't have a solution.

Examples - 2 solving linear system by different methods

Solve the following system of the linear equations by the methods a) Cramer's rule, b) by row transformation, c) by variable elimination.

2x − y + 2z = 11

x + 2y − z = −3

3x − 2y − 3z = −1

a) Solution by Cremer's rule

Solution

And the solution is:

Solution

b) Solution by row transformation

The augmented matrix will be:

Description	Operation	Result
Now multiply each value in the second row by −2 and add it to the first row.
Multiply each value in the 1st row by 3 and 3rd row by −2 and add.
Multiply 3rd row by 5 and add each item with the second row.

The last result matrix is equivalent to the equations:

Now it is clear that 64z = 192 and z = 192/64 = 3

For the second row we have: −5y + 4z = 17 and y = (17 − 4z)/−5 = (17 − 4 · 3)/−5 = −1

From the first row we have 2x − y + 2z = 11

and x = (11 + y − 2z)/2 = (11 − 1 − 2 · 3)/2 = 2

And we get the solution as before: x = 2 y = −1 z = 3

c) Solution by elimination

From the first equation we find the value of y:

From the first equation we find the value of y:	y = 2x + 2z − 11	(1)
Substitute value of y to the 2nd and 3rd equation:	x + 2(2x + 2z − 11) − z = −1
	5x + 3z = 19	(2)
	3x − 2(2x + 2z - 11) − 3z = −1
	x = 23 − 7z	(3)
Substitute equation (3) into eq. (2)	5(23 − 7z) + 3z = 19
	32z = 96
	z = 3
From eq. (3) we have	x = 23 − 7z = 23 − 21 = 2
From eq. (1) we get	y = 2x + 2z − 11 = −1

And again, the solution is as before: x = 2 y = −1 z = 3

Example - 3 Solving linear system

Solve the following system of the linear equations, investigate the answers.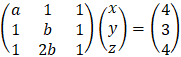

(■(a&1&1@1&b&1@1&2b&1))(■(x@y@z))=(■(4@3@4))

To make solution easier we will subtract 3rd row from the 2nd row to get the following system of equations

(■(a&1&1@1&b&1@0&b&0))(■(x@y@z))=(■(4@3@1))

By Cremer's rule we have the following determinants:

D=|■(a&1&1@1&b&1@0&b&0)|=a(-b)-0+b=b(1-a)

D_x=|■(4&1&1@3&b&1@1&b&0)|=-4b+1+(3b-b)=1-2b

D_y=|■(a&4&1@1&3&1@0&1&0)|=-a-0+1=1-a

D_z=|■(a&1&4@1&b&3@0&b&1)|=a(b-3b)-1+4b=2b(2-a)-1

The solutions are:

We can see that for valid solution we have the condition: b ≠ 0 and a ≠ 1

If b = 1/2 than the given equation is:

(■(a&1&1@1&1/2&1@1&1&1))(■(x@y@z))=(■(4@3@4))

Now we can clearly see that when a = 1 then the 1st and 3rd equations are the same.

(■(1&1&1@1&1/2&1@1&1&1))(■(x@y@z))=(■(4@3@4))

And we get only two equations for three variables as follows

(■(1&1&1@1&1/2&1))(■(x@y@z))=(■(4@3))

We can now subtract 2nd row from the 1st row to get the set of equations:

(■(1&1&1@0&1/2&0))(■(x@y@z))=(■(4@1))

From the second row we immediately see that the value of y is: y = 2 and we get from the first row the solution x = 2 − z and we see that there is infinite number of solutions.

Examples - 4 solving linear system

Solve the following system of linear equations.

3x − y + 2z = 3

2x + 2y + z = 2

x − 3y + z = 4

The augmented matrix (including free term) of this set of equations is:

(■(3&-1&2@2&2&1@1&-3&1)■(3@2@4))

by row transformation method we get:

Description		Operation		Result

Multiply 1st row by 2 and 2nd row by -3 and add both rows			→
Multiply 3rd row by -3 and add it to the 1st row			→
Add rows two and three to get the final value			→

From the result we see that the rank of the coefficient matrix (3 columns from the left - variable matrix) is R_c = 2 while the rank of the augmented matrix is R_g = 3 therefore there is no solution to this problem.

We can summarize the rules of the existence of solutions by the following facts:

a)	A linear system of m equations and n unknowns will have a solution only if the rank of the augmented matrix equals that of the coefficient matrix (R_c = R_g).
b)	If the augmented matrix and the coefficient matrix has the same rank and the rank equals the number of the unknowns, then a unique solution exist (R_c = R_g = n).
c)	If the augmented matrix and the coefficient matrix have the same rank but the rank is less then the number of unknowns (R_c = R_g < n), then at least one set of number of rank unknowns can be solved in terms of the remaining (n - r) unknowns.

Examples - 5 solving homogeneous linear system

Solve the following homogeneous system of linear equations.

2x − y + z = 0

x + 2y + 3z = 0

3x + y + 4z = 0

It is obvious that the trivial solution is: x = y = z = 0, we can say that every system of linear equations have that solution. Notice that the rank of the coefficients and the augmented matrix are the same.

Description		Operation		Result

Multiply 2nd row by −2 and add it to 1st row			→
Subtract first row from the third row			→

And we get the final set of equations

(■(2&-1&1@0&-5&-5@0&0&0))(■(x@y@z))=(■(0@0@0))

The rank of the coefficients and the augmented matrices are the same and equal to, R_c = R_g = 2

Because the number of variables is 3 then R is less then n (2 < 3) and we have a non zero solution which depends on the value of the third variable that can get infinite number of values:

y = −z and x = −z for example if z = −1 then the result is (1, 1, −1)

Examples - 6 solving linear system

Solve the following system of linear equations

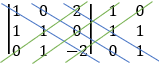
We will find the determinant value D by the diagonal method:

Linear system - example 6

Copy the first two columns to the end of the matrix and the result is the multiply of the 3 values alone the line so that the multiplication

D = 1· 1 · (− 2) + 0 · 0 · 0 + 2 · 1 · 1 − 2 · 1 · 0 − 1 · 0 · 1 − 0 · 1 · (− 3) = 0

The determinant is equal to 0 so we have at least two identical rows.

Description		Operation		Result

Subtract first row from the second row			→
And we get the final set of equations			→

The system of equations is now:

Because R_c = R_g = 2 and number of variables is n = 3 < R_g then 2 variables can be expressed by the third variable, and we get infinite number of solutions:

The set of equations are:	And the solutions are:
x + 2z = 1	x = 1 − 2z
−y + 2z = −1	y = 2z + 1

Notice that the solution of x and y are a function of any value of z.