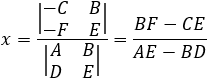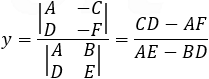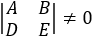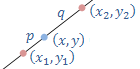☖ Home ⇄ Units Converter ⧉ Geometry Σ Math ✈ Physics 〶 Electricity

2D Line calculator

Print line calculator
Line general equation:
 y =  
 x + 
 x +  
 y + 
 = 0
Line defined by 2 points:
(x1 , y1)
( ,
)
(x2 , y2)
( ,
)
Line defined by a point and an angle:
(xp , yp):
( ,
 )
Angle:
Degree
Distance from the point (xt,yt) to the inputed line:
(xt , yt):
( ,
 )
Distance (D):
Line definition
Input line:
Line angle:
Distance from the inputed line to the origin:
Intercepts of input line:
x: intercept (
 ,  0)
y: intercept (0
 , 
)
Perpendicular line from (x,y) to the given line:
Intersection of the given and perpendicular line:
Degree Radian     
Line basic definition
Line distances
Intersection point ex: 3
Basic line information
Distance from point ex: 1
Line equations
Perpendicular line ex: 2

Line summary

Print lines basic definition
Single line
Line definition
Two lines intersection
Two lines intersection
Line most general equation is of the form:
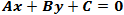
      (1)

where  A, B  and  C  are any real number and  A  and  B  are not both zero. If  B ≠ 0  then we can divide

equation (1)  by  B  to obtain the normalized form of a line:
y=-A/B x-C/B
      (2)
This is the equation of a line whose slope is:
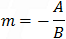
Line slope
and
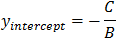
Line intercept
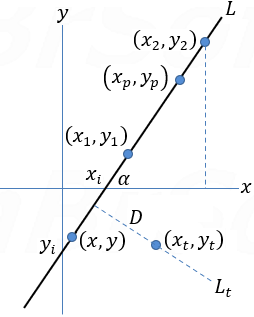
the slope of the line (m) is defined in terms of the inclination
m=tan⁡(α)=(y_2-y_1)/(x_2-x_(1))
      (3)

Note: if the angle α is greater then 90 degrees then the slope is negative.

α (0 - 90) degrees   : positive slope
α (90 - 180) degree   : negative slope
Necessary condition for two lines to be perpendicular to each other is that their slopes fulfill the condition:
m1 m2 = − 1
      (4)

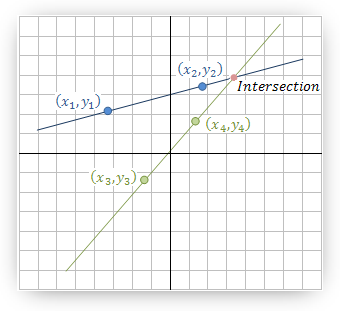
In order to find the intersection point of two lines we have to solve the system of linear equations representing the lines. A x + B y = −CD x + E y = −F

solution by matrix:
Matrix solution of a line
Matrix solution of a line
If the determinant:
  Line solution determinant
  then intersection point exists.

Basic information about line of the form     y = ax + b     or     Ax + By + C = 0

Print lines basic definition
Slope (m) of the line
m = a Slope m Slope m Slope m
yintercept (yi)
yi = b yi = −mxi yi = y1 − mx1 y intercept
xintercept (xi)
x intercept x intercept x intercept x intercept
tan θ
tan θ = m tan θ tan θ
Line angle (θ)
from x axis (range 0 ≤ θ < π)
θ = arctan(m) θ = arctan(m) θ = arctan(m)
Slope (M) of a line perpendicular to a given slope (m)
Slope of perpendicular line Slope of perpendicular line Slope of perpendicular line Slope of perpendicular line
Line midpointLine point
tan θ
Point (x, y) which divides the line connecting two points (x1 , y1) and (x2 , y2) in the ratio p:q
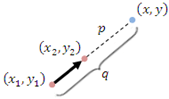
Portion of a line Portion of a line
Point (x, y) which divides the line connecting two points (x1 , y1) and (x2 , y2) externally at a ratio p:q
Portion of a line tan θ
Note: the (x,y) point is in the direction from point 1 to point 2,to get the other side extension change the point 1 with point 2 and vice versa
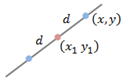
A point (x, y) which is located at a distance d from a point (x1 , y1) on the line
Distance from a line
Angle θ between two lines:
Angle limit
(Slopes)
Angle between two slopes
(2 Points)
Angle between two lines
Angle between two lines:
Ax + By + C = 0
Dx + Ey + F = 0
Angle between two lines Angle between two lines

Line equations summary

Print lines basic equations
Equation of a line passing through a point (x1 , y1)
y = mx + ( y1 − mx1) y − y1 = m(x − x1)
Equation of a line passing through two points (x1 , y1), (x2 , y2)
Line passing through two points Line passing through two points
Equation of a line perpendicular to a given slope m and passing through a point (xp , yp)
Equation of a line perpendicular to a given slope Equation of a line perpendicular to a given slope
Equation of a line perpendicular to a line which is defined by two points (x1 , y1) and (x2 , y2) and passing through the point (xp , yp)
Perpendicular line Perpendicular line
Equation of a line passing through the intercepts xi , yi
Intercepts point xiy = −yix + xiyi
Equation of a line passing through the point (xp ,yp) and parallel to a line which is defined by two points (x1 , y1) and (x2 , y2)
Line passing through a point Line passing through a point
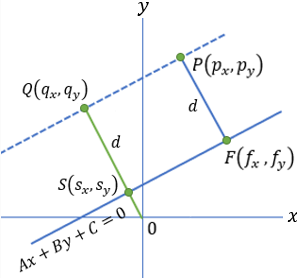
Equation of a line parallel to the line Ax + By + C = 0 and at a distance d from it.
Parallel line
Equation of the midline between the lines    Ax + By + C = 0
Dx + Ey + F = 0
Midline
Equation of a line perpendicular to the line    Ax + By + C = 0
Bx − Ay + C = 0
Equation of a horizontal line
Horizontal line y = b
Equation of a vertical line
Vertical line x = a

Lines distances     y = ax + b    Ax + By + C = 0

Print lines distances
Distance between two points (D)
Points distance
Distance between intercepts xi and yi
Intercepts distance
Distance from a line to the origin
Origin distance
Origin distance
Distance from a line given by two points (x1 ,y1),(x2 , y2) to the origin
Line distance
Distance from a line to the point
(xp , yp)
Line point distance
Line point distance
Distance from a line given by two points (x1 , y1) , (x2 , y2) to the point (xp , yp)
Line point distance
Distance between two parallel lines
y = ax + by = cx + d
or
Ax + By + C = 0Dx + Ey + F = 0
Parallel lines
Parallel lines
Example 1 - distance from a line to a point Print vertices and eccentricity example ▲
Find the distance  d  of a point   P(px , py)   from the line given by the equation   Ax + By + C = 0.
And calculate the numerical value of the distance between point  (2 , −3)  and line  y = 4x − 5
Sketch ex 1
We draw at point  P  a parallel line to the given line (dashed line).
Then we draw a line  PF  between the points  P  and  F. This line is perpendicular to the given line.
The slope m of the given line is: m = −A / B
The slope M of line PF is: M = −1 / m = B / A
In order to make calculations easier we draw another line  QS  starting from the origin and parallel to line  PF.
The general equation of a line passing through a point is given by:      y = mx + y1 − mx1
The equation of line  PQ  passing through point  (px , py)  is: y=-A/B x+p_y+A/B p_x
Equation of line  QS  passing through the origin is: y=B/A x
Point  Q  is the intersection of lines  PQ  and  QS.  Solving this equations by substituting the value of  y  we get: B/A x =(-Ax+Ap_x+Bp_y)/B
And finally, we get: x=(A^2 p_x+ABp_y)/(B^2+A^2 ) and y=(ABp_x+B^2 p_y)/(B^2+A^2 )
Point  S  is the intersection point of the two lines Ax + By + C = 0 and y=B/A x
Solving for  Sx  and  Sy  we get Ax+B B/A x+C=0
x=-AC/(A^2+B^2 ) and y=-B/A AC/(A^2+B^2 )=-BC/(A^2+B^2 )
The distance  d  is the distance between the two points  Q  and  S  given by the points:
Q((A^2 p_x+ABp_y)/(B^2+A^2 ),(ABp_x+B^2 p_y)/(B^2+A^2 )) and S(-AC/(A^2+B^2 ),-BC/(A^2+B^2 ))
d=√((S_x-Q_x )^2+(S_y-Q_y )^2 )
d=√(((A^2 p_x+ABp_y)/(B^2+A^2 )+AC/(A^2+B^2 ))^2+((ABp_x+B^2 p_y)/(B^2+A^2 )+BC/(A^2+B^2 ))^2 )
d=√(A^2 (Ap_x+Bp_y+C)^2+B^2 (Ap_x+Bp_y+C)^2 )/(A^2+B^2 )
d=√((Ap_x+Bp_y+C)^2 (A^2+B^2 ) )/(A^2+B^2 )
d=|Ap_x+Bp_y+C|/√((A^2+B^2 ) )
The given line can be written in the standard form as       4x − y − 5 = 0
So, we have:       A = 4       B = −1     and     C = −5        px = 2       py = −3
Substituting these values into the distance equation we get the final solution:
d=|4∙2+(-1)(-3)-5|/√((4^2+(-1)^2 ) )=|8+3-5|/√17=6/√17=1.46
Example 2 - line from point to perpendicular line Print line from point to perpendicular line example ▲
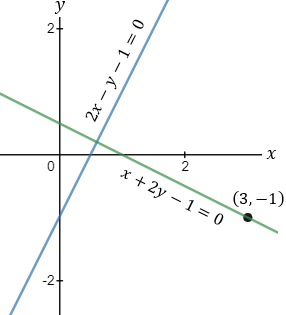
Find the equation of the line passing through the point   (3 , − 1)   and is perpendicular to the line
2x − y − 1 = 0
Sketch ex 2
The slope of the perpendicular line is:
y = 2x − 1 → m = 2
The slope of the line perpendicular to the given line and passing through the point is:
M=-1/2
The equation of the line passing through the point  (3 , − 1)   is:
y = Mx + (y1 − Mx1)
y=-1/m x+y_1+1/m x_1
y=-1/2 x-1+1/2∙3
x + 2y − 1 = 0
If the intersection point of both lines is needed then we have to solve the equations:
x + 2y − 1 = 0
2x − y − 1 = 0
From the first equation x is x = 1 − 2y
Substitute x into the second equation 2(1 − 2y) − y − 1 = 0
And the intersection coordinate is (0.6 , 0.2)
Example 3 - intersection point of perpendicular lines Print intersection point between line and point example ▲
Find the intersection point of the line   2x − y = 0   and the line passing through the point (5 , 2)   and is perpendicular to the given line.
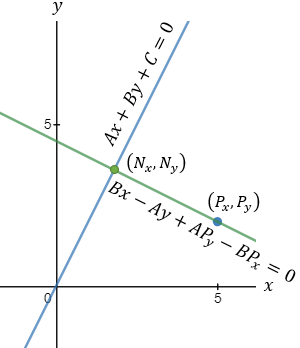
Sketch ex 3
If the line form is given by:     Ax + By + C = 0
The slope of the given line is: m = − A/B
Slope of the line perpendicular to the given line is:
M=B/A=(-1)/2=-0.5
The equation of the line passing through the point   (Px , Py) = (5 , 2)   (green line) and is perpendicular to the given line is:
y = Mx + (Py − MPx)
y=B/A x+P_y-B/A P_x (1)
y = −0.5x + 2 + 0.5‧5 (2)
x + 2y − 9 = 0
In order to find the intersection point (Nx , Ny) we have to solve equation (1) and the given line this can be done in direct substitution or by Cramer’s law:
From equation (1) We have y=-A/B x-C/B
Substitute  y  into equation (1) -A/B x-C/B=B/A x+P_y-B/A P_x
Solving for  x  we get x=(B^2 P_x-ABP_y-AC)/(A^2+B^2 )
And  y  is equal to x=(B^2 P_x-ABP_y-AC)/(A^2+B^2 )
The general intersection of a line and the perpendicular line that passes through a point is:
((B^2 P_x-ABP_y-AC)/(A^2+B^2 ) ,-1/B [(〖AB〗^2 P_x-A^2 BP_y-A^2 C)/(A^2+B^2 )-C]) (3)
The given values are     A = 2       B = −1       C = 0       Px = 5       Py = 2
Solving the numerical values, we have
x + 2(2x) − 9 = 0
x = 9/5 = 1.8
and y is equal to
y = 18/5 = 3.6