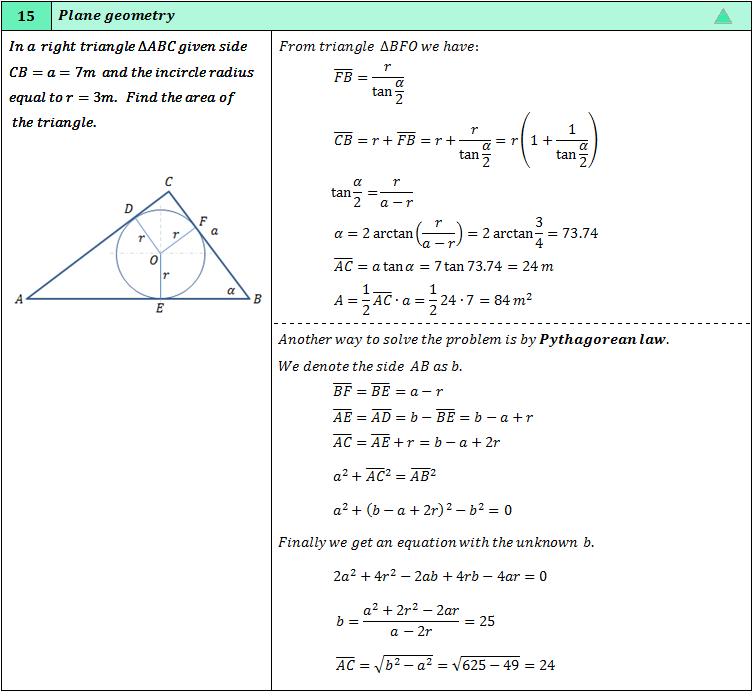
Plane geometry solved examples
















Example 18a - proof of bisector theorem
Proof the bisector theorem.
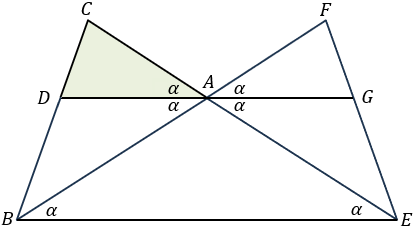 Set the bisector line DA to horizontal position and extend the triangle ABC in the opposite direction to get triangle AFE. Because AD || BE (parallel lines). The triangles ADC ⁓ BCE are similar and
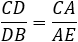 Because AE = AB we get the general form of the angle bisector theorem. 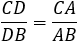 Example 18b - triangle bisector
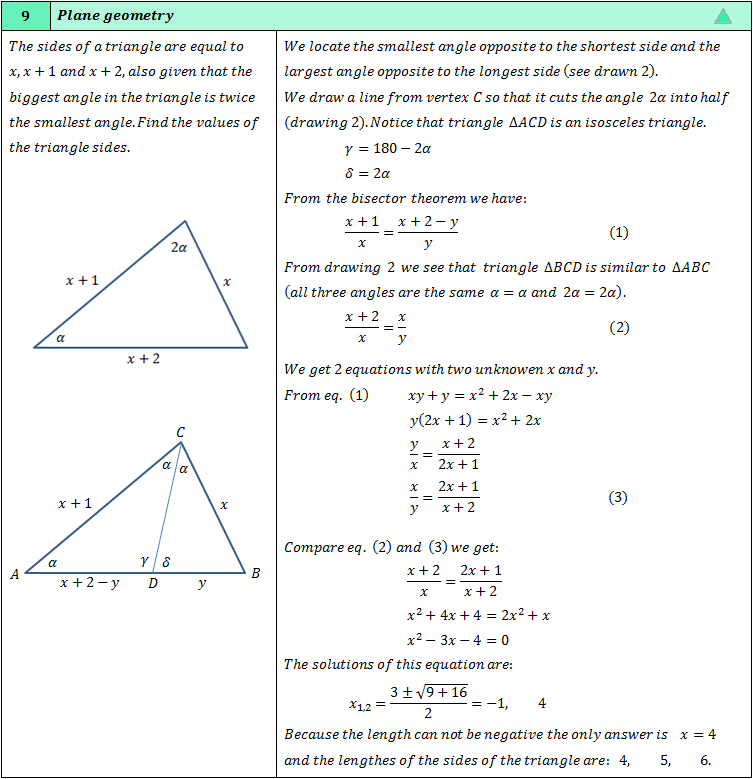
The sides of a triangle are equal to x, x + 2 and x + 4, it is also known that the smallest angle is equal
to α and the largest angle is 2α. Find the lengths of the triangle sides.
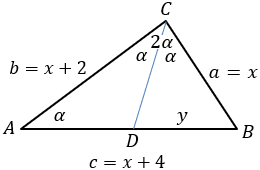 Draw the bisector line from vertex C to the side AB and mark the intersection point as D. Also mark the length of segment BD as y. Notice that triangle ACD is isosceles whose side AD is equal to: AD = AB − y = x + 4 − y According to the angle bisector theorem we have the relation 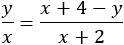 (1)
Realise that the triangles ACB and triangle CBD are similar triangles based on three equal angles. 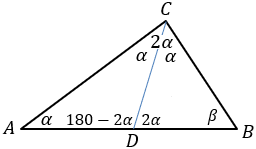 Angles of triangle ACB are α, 2α, β
Angles of triangle CDB are α, 2α, β
So, both triangles are similar: ACB ⁓ CDB and we have
DB / BC (sides facing α angles) equal to
BC / AB (sides facing 2α angles) That is:
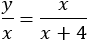 (2)
Solving equations (1) and (2) for x and y we get the quadratic equation: x2 − 6x − 16 = 0 The solution of this equation is x = 8 (other solution x =-2 is irrelevant) and the sides of the triangle are 8, 10 and 12. 






|
