☖ Home ⇄ Units Converter ⧉ Geometry Σ Math ✈ Physics 〶 Electricity

Quadratic, Cubic, Quartic Equations calculator

Print quadratic equations calculator
 
  
  ╂ 
  
  ╂ 
  
  ╂ 
  
  ╂ 
  
Solutions
X1 =
X2 =
X3 =
X4 =
Input Equation:
First Derivation:
Second Derivation:
Extreme points
x value
y value
position
1
2
3
First root
x1 
Second root
x2 
Quadratic equation is:

Quadratic, cubic, quartic equations summary

Print quadratic equations summary
Quadratic equation is of the form:        f(x) = ax2 + bx + c = 0
This equation has two solutions defined by:
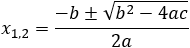
The value under the root:    b2 - 4ac   is called the discriminant (Δ).
When   Δ > 0   then two real solutions exist.
When   Δ = 0   then one real solution exists.
When   Δ < 0   then two complex solutions exist.
The roots are related to each other by the formulas:
To find the extreme points of the graph we must
find the first derivation of the function and compare it to 0.
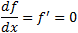
To find if the extreme point is a maximum or minimum of
the graph we must find the second derivation of the function.
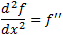
If   f '' > 0   then the extreme point is a minimum.
If   f '' < 0   then the extreme point is a maximum.
Example 1: Find the extreme point of the function     f(x) = x2 + 3x - 10 = 0
Print example 1
The solutions of the function are:
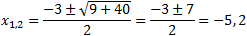
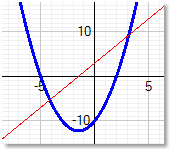
First derivation is:    f ' = 2x + 3 = 0    extreme point at   x = -1.5
Second derivation is:   f '' = 2   
because   f '' >0   the extreme point is a minimum.
Example 2: Find the extreme points of the function   f(x) = 4x4 + 4x3 - 11x2 + 2x + 10 = 0
Print example 2

The solutions of the equation are:       −0.849,   −2.139,   0.994 ± i0.623

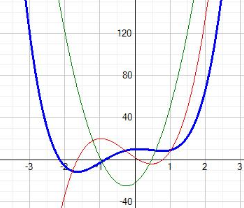
First derivation is:    f ' = 16x3 + 12x2 - 22x + 2 = 0
(This curve is sketched by the red line)
The solutions of first derivation will give us the extreme points
which are at:    x1 = -1.64,    x2 = 0.1    x3 = 0.79
To find if the points are a maximum or minimum, we
shall find the second derivation:       f ''(x) = 48x2 + 24x - 22
Now substitute each extreme point to the second derivation:
f '' (x1) = 48 * (-1.64)2 + 24 * (-1.64) - 22 = 67.7
f '' (x2) = 48 * 0.12 + 24 * 0.1 - 22 = -19.1
f '' (x2) = 48 * 0.792 + 24 * 0.79 - 22 = 26.9
x1 - is minimum,    x2 - is maximum,    and x3 - is minimum.
Example 3: Find the quadratic equation if we know that the roots are 2 and 3.
Print example 3

The general form of the quadratic equation is found by the following steps.

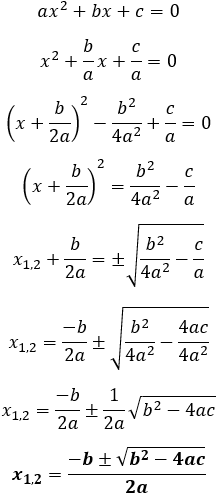
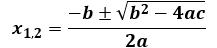
x_(1,2)=(-b±√(b^2-4ac))/2a
x_(1,2)=(-b±√(b^2-4ac))/2a
(1)

Now we can add and multiply solutions  (1)  to get the result of  x1  and  x2  as a function of the coefficients  a,  b  and  c  as follows.

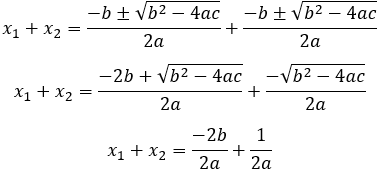
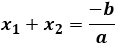
x_1+x_2=(-b)/a x_1 x_2=c/a
x_1+x_2=-b/a
(2)
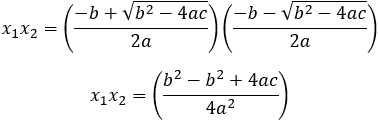
x_1+x_2=(-b)/a x_1 x_2=c/a
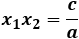
x_1∙x_2=c/a
(3)

Substitute given solutions  x1 = 2  and  x2 = 3  into equations  (2)  and  (3). 

b = −(x1 + x2)a = −(2 + 3)a = −5a

c = x1x2a = 2 ‧ 3a = 6a

If we chose  a = 1  than the quadratic equation will be:       x2 − 5x + 6 = 0