AmBrSoft.net Ellipse calculator

Ellipse with center at (h , k) calculator

x² +

y² +

x +

y +

= 0

(x −	)²	+	( y −	)²	= 1

2			2

Polar form: the left focus point is at the origin:

Semi-major axis (a)

Semi-minor axis (b)

Area (A)

Eccentricity (e)

Foci length (c)

Flattening factor (f)

Foci location

vertices locations

Ellipse center

Perimeter (P)

Input limit:
Notes:

Line tangent to ellipse

A point on the ellipse

x₁ y₁

Tangent line slope m = tanθ:

Line angle θ :

	Tangency point	Tangent line equation	Line angle
Point 1
Point 2

Summary center (0,0)
Summary center (h,k)
1. Ellipse equation
2. Tangent line
3. Ellipse tangent line
4. Vertices and eccentricity

5. Vertices and eccentricity
6. Foci and eccentricity
7. Ellipse center at (x,y)
8. Ellipse equation
9. Ellipse equation forms
10. Area of ellipse

11. Ellipse tangent lines 1
12. Ellipse tangent lines 2
13. Minor and major axes
14. Ellipse and tangent points
15. Distance from foci

Ellipse with − center at (0 , 0) summary

An ellipse is the locus of all points that the sum of whose distances from two fixed points is constant,

d₁ + d₂ = constant = 2a

the two fixed points are called the foci (or in single focus).

distance between both foci is: 2c

a and b − major and minor radius

Equation of a horizontal ellipse is:

(center at x = 0 y = 0)

Equation of a vertical ellipse is:

(Center at x = 0 y = 0)

Notice that the values of a and b has swapped, this was done in order to keep the value of the vertex as a (see drawing). Keep in mind that in order to calculate the slope of the tangent line do not take the swapped values.

The eccentricity e of an ellipse is:

(a > b)

Where (c = half distance between foci) c < a 0 < e < 1

If	e = 0	then the ellipse is a circle.
If	0 < e < 1	then it is an ellipse.
If	e = 1	then the ellipse is a parabola.
If	e > 1	then the ellipse is a hyperbola.

The flattening f of an ellipse is the amount of the compression of a circle along a diameter to
form an ellipse and its value is:

Notes: (1) When a = b then f = 0 it means that the ellipse is a circle. (2) In vertical ellipse the values of a and b should be swapped.

The vertices of an ellipse are the intersection points of the major axis and the ellipse. The line segment joining the vertices is the major axis, and its midpoint is the center of the ellipse.

For a horizontal ellipse	( a > b ) vertices are at:	(a , 0) and (−a , 0)
For a vertical ellipse	( b > a ) vertices are at:	(0 , a) and (0 , −a )

From ellipse definition d + d = const

And from x direction 2c + 2(a − c) = const

2d = 2a

And we get the relation d = a and:

The points A₁ and A₂ in this case (±a , 0) are the vertices of the major axis.

The slope of the tangent line to the ellipse at point (x₁ , y₁) is:

The tangent line equation at a point (x₁ , y₁) on the ellipse

Note: In this equations do not change between a and b even if b > a

The area of an ellipse is exactly:

A = πab

Example of ellipse area

The perimeter (P) of an ellipse is found by integration:

The only solution is by series:

Where e is the eccentricity of the ellipse

Another solution is by using the series:

Where

Ramanujan approximation for the circumference:

Where

Less accurate approximation

Ellipse with − center at (h , k) summary

If the center of the ellipse is moved by x = h and y = k then if a point on the ellipse is given the corresponding x or y coordinate is calculated by the equations:

Ellipse equation	Given	Equivalent point on ellipse
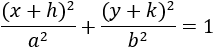	x₁
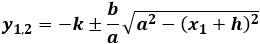	y₁

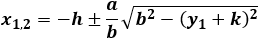Notice: these equations are good for horizontal and vertical ellipses.

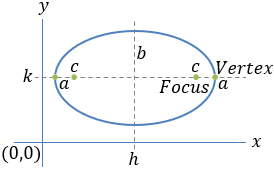
Ellipse
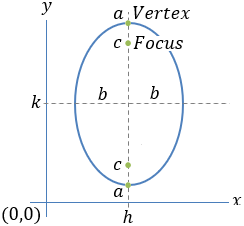Center	(h , k)	(h , k)
Vertices	(h − a , k) (h + a , k)	(h , k − a) (h , k + a)
Foci	(h − c , k) (h + c , k)	(h , k − c) (h , k + c)

The slope of the line tangent to the ellipse at point (x1 , y1) is:

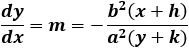
The equation of the tangent line at point (x1 , y1) on the ellipse is:

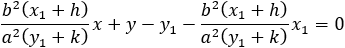
(b^2 (x_1+h))/(a^2 (y_1+k) ) x+y-y_1-(b^2 (x_1+h))/(a^2 (y_1+k) ) x_1=0

Or:

y=-(b^2 (x_1+h))/(a^2 (y_1+k) ) x+y_1+(b^2 (x_1+h))/(a^2 (y_1+k) ) x_1

Converting ellipse presentation formats: (See detail calculation example)

①

Ax² + By² + Cx + Dy + E = 0

②

① → ②	Define:

② → ①

A = b²

B = a²

C = 2hb²

D = 2ka²

E = a²k² + b²h² − a²b²

Polar coordinate of ellipse:

Any point from the center to the circumference of the ellipse can be expressed by the angle θ in the

range (0 − 2π) as:

x = a cosθ y = b sinθ

If we substitute the values x = r cosθ and y = r sinθ in the equation of the ellipse we can get the

distance of a point from the center of the ellipse r(θ) as:

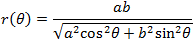If the origin is at the left focus then the ellipse equation is:

Example 1 − Verify the equation of an ellipse

From the definition of the ellipse, we know that d₁ + d₂ = 2a

Where a is equal to the x axis value or half the major axis.

From the drawing d₁ and d₂ are equal to:

Simplify the equation by transferring one radical to the right and squaring both sides:

After rearranging terms, we obtain:
We square again both sides to find:
After arranging terms, we get:
Dividing by a² − c² we find:
Since a > c we can introduce a new quantity:
And the equation of an ellipse is revealed:

If the foci are placed on the y axis then we can find the equation of the ellipse the same way: d₁ + d₂ = 2a

Where a is equal to the y axis value or half the vertical axis.

From the drawing d₁ and d₂ are equal to:

After arranging terms and squaring we get:
After rearranging terms, we find:
Set new quantity (see above):
Dividing by b² we get the final form:

Example 2 − Tangent line to an ellipse with center at (h , k)

Find the equations of the tangent lines at the points of the intersection of line x = 5.5 and the ellipse

First we will solve the general case of the tangent line to the ellipse.

The slope of the tangent line by explicit derivation:

And the slope value at a point on the ellipse is:
The tangent line equation at point (x₁ , y₁) is:	mx − y + (y₁ − mx₁) = 0

After rearranging terms:

b² (x₁ + h) x + a² (y₁ + k) y − a² (y₁ + k) y₁ − b² (x₁ + h) x₁ = 0

Notice that if the ellipse is located in the origin than h = k = 0 and the line equation turns to be

b²x₁x + a²y₁y − a²y₁² − b²x₁² = 0

Now we will find the two points y_1,2 of the intersection of the given line x = 5.5 with the ellipse.


	9 (5.5 − 4)² + 3(y + 5)² = 27
After solving for y we get
The intersection points are:	(5.5 , − 3.5) (5.5 , − 6.5)

Now we have to find the slope of the tangent line to the ellipse by implicit derivation.

After derivation we get:
And the slope m is:

The slopes of the tangent lines at the two tangent points are:

Now we can find the equation of the tangents lines according to slope and a point.

First line:	mx - y + y₁ − mx₁ = 0	→	-3x - y − 3.5 + 3 * 5.5 = 0	→	3x + y − 13 = 0
Second line:	mx - y + y₂ − mx₂ = 0	→	3x - y − 6.5 + 3 * 5.5 = 0	→	3x − y − 23 = 0

Example 3 − Tangent line to an ellipse

Find the equation of the line tangent to the ellipse 4x² + 12y² = 1 at the point P(0.25 , 0.25).

By implicit differentiation we will find the value of dy/dx that is the slope at any x and y point.

Implicit differentiation dy/dx is:
The value of dy/dx is:
At the given point the slope is:
Equation of the tangent line that passes through the point P and has slope m is: y = mx + ( y_p − mx_p)
Substitute the point P(0.25 , 0.25) we get:	y = mx + (0.25 - m * 0.25)
And the tangent line equation is:	x + 3y − 1 = 0

Example 4 − vertices and eccentricity

Given an ellipse by the equation 81x² + 4y² = 324 find the eccentricity, flattening, area and the focus distance c of the ellipse.

Divide by 324. to obtain
Since a < b ellipse is vertical with foci at the y axis and a = 9 and b = 2.

Eccentricity:		Flattening:
Focus c:	c = a * e = 8.775	Area:	A = π2∙9 = 56.55

Example 5 − vertices and eccentricity

Find the equation of the ellipse that has vertices at (0 , ± 10) and has eccentricity of 0.8.

Notice that the vertices are on the y axis so the ellipse is a vertical ellipse and we have to use the vertical ellipse equation.

The equation of the eccentricity is:
After multiplying by a we get:	e²a² = a² − b²
The value of b² is:	b² = a²(1 − e²)
The equation of a vertical ellipse is:
And the final equation of the ellipse is:

Example 6 − foci and eccentricity

Find the equation of the ellipse that has eccentricity of 0.75, and the foci is along the x axis and second time if the foci is along the y axis, ellipse center is at the origin, and passing through the point (6 , 4).

The point (6 , 4) is on the ellipse therefore fulfills the ellipse equation.

1.	Substitute the point (x₁ , y₁) into the ellipse equation (foci at x axis):
	From the previous example:	b² = a²(1 − e²)
	Substitute b² into ellipse equation:
	The value of a² is:
	The value of b² is:
	And the equation of the ellipse is:	7x² + 16y² = 508

2.	Vertical ellipse equation is (foci at y axis):
	Substitute b² into ellipse equation:
	The value of a² is:
	The value of b² is:
	And the equation of the ellipse is:	16x² + 7y² = 688

Example 7 − Translated center of ellipse

Find the vertices and the foci coordinate of the ellipse given by 3x² + 4y² − 12x + 8y + 4 = 0.

Find the square in x and y:	3(x² - 4x ) + 4(y² + 2y ) = − 4
Add and subtract 4 to the left parentheses and 1 to the right parentheses to obtain:
	3(x − 2)² − 12 + 4(y + 1)² − 4 = − 4
	3(x − 2)² + 4(y + 1)² = 12

After dividing by 12 we get:

The center of this ellipse is at (2 , − 1) h = 2 and k = − 1.

Translate the ellipse axes so that the center will be at (0 , 0) by defining:

x' = x − 2

y' = y + 1

now the ellipse equation in the x'y' system is:

Which we recognize as an ellipse with vertices a = ± 2

and the foci is

In the xy system we have the vertices at (2 ± 2 , − 1) and the foci at (2 ± 1 , − 1).

The sketch of the ellipse is:

Example 8 − Ellipse center

Find the equation of the locus of all points the sum of whose distances from (3, 0) and (9, 0) is 12.

It can be seen that the foci are lying on the line y = 0 so the ellipse is horizontal.

The focus is equal to:

From the definition of the ellipse, we know that:	d₁ + d₂ = 2a
and the value of a is 12 = 2a	a = 6
and the value of minor vertex b is:

The ellipse in the x'y' system is:
The ellipse in the xy system is:
The ellipse after rearranging terms is:	3x² + 4y² − 36x = 0

Example 9 − Converting ellipse presentation formats

Find the equation of the translation between the two forms of ellipse presentation.

①

Ax² + By² + Cx + Dy + E = 0

②

From equation ② we have:	b² ( x + h )² + a² ( y + k )² = a²b²
	b² ( x² + 2hx + h²) + a²( y² + 2ky + k²) = a²b²
And finally:	b² x² + 2b²hx + b²h² + a²y² + 2a²ky + a²k² − a²b² = 0
After rearranging by powers:	b² x² + a² y² + 2b²h x + 2a²k y + b²h² + a²k² − a²b² = 0

Now we can find the values of the coefficients of the ellipse equation ① A, B, C, D and E.

A = b²

B = a²

C = 2b²h

D = 2a²k

E = b²h² + a²k² − a²b²

The transformation from equation ② to equation ① includes more steps to solve:
From equation ① we have:	(A x² + C x) + (B y² + D y) = −E

Take A and B out of both parenthesis:

Now we use the square formula of the form x² + 2Rx + R² = (x + R)² to get the square equations:

We have to add the following values to the right side of the equation:

(3)

In order to simplify the equation, we set:

We get:

A (x + h)² + B (y + k)² = − E + A h² + B k²

Simplify again by setting the value: φ = − E + A h² + B k² to get the equation:

A (x + h)² + B (y + k)² = φ

(4)

Divide equation (4) by AB:

(5)

Divide both sides of equation (5) by the value of the right side of (5) φ/AB the result is:

We got the equation of the ellipse where h and k are the center of the ellipse and the denominators are the square values of the semi major and minor length a² and b² the complete transformation are:

Example 10 − area of an ellipse

Find the area of an ellipse if the length of major axes is 7 and the length of minor axes is 4

Example of finding area of ellipse

(see integral solution)

Example 11 − tangent lines to ellipse

Find the slope and the tangent line equation at a point where x₁ = 2 on the ellipse

The general equation of an ellipse with center at (0 , 0) is:

Implicit differentiation of the ellipse equation relative to x:

Eliminating

= m (slope) from the derivation yields:

Line equation at point (x₁ , y₁) is:

y − y₁ = m (x − x₁)

(1)

Substitute the value of m (slope of the line dy/dx) into equation (1) to get the equation of the line tangent to the ellipse at point (x₁ , y₁):

Multiplying all terms by a² y₁

a² y y₁ − a² y₁² = −b² x x₁ + b² x₁²

(2)

Point (x₁ , y₁) is on the ellipse therefore it satisfies the ellipse equation:

Substitute x<sub>1</sub> and y<sub>1</sub> into ellipse equation

(3)

Substitute eq (3) into eq (2) we get the general form of a tangent line to an ellipse at point (x₁ , y₁)

b² x₁ x + a² y₁ y − a²b² = 0

(4a)

Or after dividing by a² y₁ we get:

General tangent line to ellipse equation

(4b)

Now we should find the tangent points where x₁ = 2 therefore substitute the point x₁ in the equation of the ellipse and eliminate y we should get two values for y corresponding to the upper and lower sides of the ellipse (see sketch below).

The slopes of the tangent lines are:

Notice that when point y₂ is negative then the slope m is positive and vies versa.

from eq (4b) the equations of the tangent lines are:

y = − 0.43 x + 3.46

y = 0.43 x − 3.46

Example 12 − tangent lines to ellipse

Find the equation of the line tangent to the ellipse 4x² + 12y² = 1 at the point P(0.25 , 0.25).

The slope of the tangent line

can be found by implicit derivation of the ellipse equation:

Eliminate dy/dx to obtain:

The slope at point x = 0.25 is:

(slope of the tangent line)

The tangent line equation at the given point is:	y − y₁ = m (x − x₁)
Substitute given values for x₁ and y₁:
And finally tangent line equation is:	x + 3y − 1 = 0

Example 13 − foci and minor and major axes

Given the ellipse 4x² + 9y² − 16x + 108y + 304 = 0 find the lengths of the minor and major axes, the coordinates of the foci and eccentricity.

Completing the square for both x and y we have

(4x² − 16x) + ( 9y² + 108y) + 304 = 0

(2x − 4)² − 16 + (3y + 18)² − 324 + 304 = 0

4(x − 2)² + 9(y + 6)² = 36

Divide by 36:

which tells us that a = 3, b = 2

From the ellipse equation we see that the center of the ellipse is at: (2 , −6)

Since a² = b² + c² we find that

And the first focus coordinate on the x axis is:

And the second focus coordinate on the x axis is:

The eccentricity (only the positive value) is:

Notice that a, b, h and k can be found by using the equations that had been derived earlier:

Substituting all values to the equation of the ellipse we get:

Example 14 − distance of a line from ellipse

Given the ellipse 16x² + 25y² = 400 and the line y =−x + 8 find the minimum and maximum distance from the line to the ellipse and the equation of the tangents lines.

Divide the ellipse equation by 400 to get the general form of the ellipse, we can see that the major and minor lengths are a = 5 and b = 4:

The slope of the given line is m = −1 this slope is also the slope of the tangent lines that can be written by the general equation y = −x + c (c is a constant). Because the tangent point is common to the line and ellipse we can substitute this line equation into the ellipse equation to get:.

Completing the square for both x and y we have	(4x² − 16x) + ( 9y² + 108y) + 304 = 0
	41x² − 50cx + 25c² − 400 = 0
And the solution of this square equation is:

Notice that two different solutions for x will give us intersection of an ellipse and a line therefore we need only one solution for tangency condition that will happen when the expression under the root will be equal to 0.

65600 − 1600c² = 0

and

The general tangent line equation is:

y = mx + c

substitute m = − 1 and c_1,2 into this equation will give us the two tangent lines which are:

x + y + 6.4 = 0

and

x + y − 6.4 = 0

Distances d and D (see drawing) are the distances between the tangency lines and the given line and can be found according to the equation for the distance between two lines:

where line equations are:

Ax + By + C = 0

and

Dx + Ey +F = 0

In our case A = B = C = 1 so the distance reduces to:

Example 15 − distance from a point on ellipse to foci

Find the points on the ellipse

whose distance from the right foci is 6.

Foci values are:
Foci coordinates are:	(− 4 , 0) and (4 , 0)
From ellipse definition we have:
d₁ + d₂ = 2c + 2(a − c) = 2a
After substitute d₂ = 5 we get d₁ = 2a − 6 = 10 − 6 = 4
Points (x₁ , y₁) and (x₂ , y₂) can be found geometrically.

x₁ = c − d₂ cosθ

(1)

The value of cosθ can be calculated from cos law:

d₁² = d₂² + 4c² − 2 cosθ 2cd₂	(2)

From eq. (1)	x₁ = 4 − 6 · 0.875 = −1.25
	y₁ = d₂ sinθ = 6 • 0.484 = 2.9
The points on ellipse that are 6 units from the foci are:
(−1.25 , 2.9) (−1.25 , −2.9)

The answer can be checked by calculating the distance between the calculated point and the foci.

d=√((x_1-x_f )^2+(y_1-y_f )^2 )=√((4+1.25)^2+(2.9-0)^2 )=6

Another way to solve the problem is to find the intersection points of a circle whose radius is d₂ and with center at the right foci and the given ellipse.

(x − c)² + y² = d₂²
From ellipse equation we have:
Substitute y² into the circle equation we get:

We get a quadratic equation for the x coordinate:

0.64x² −8x −11 = 0

The solutions of this equation are: −1.25 and 13.75 the second solution is located outside the ellipse so the only solution is x₁ = −1.25 as expected.

The value of y coordinate can be calculated from the ellipse equation: