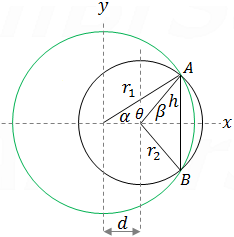
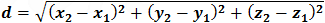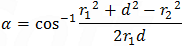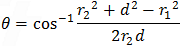☖ Home ⇄ Units Converter ⧉ Geometry Σ Math ✈ Physics 〶 Electricity

Two spheres intersection

First sphere
Sphere form:     (x - a)2 + (y - b)2 + (z - c)2 = r2
(x − )2 + (y − )2 + (z − )2 = 2
Sphere form:     x2 + y2 + z2 + Ax + By + Cz + D = 0
x2 + y2 + z2 + x + y + z + = 0
Second sphere
Sphere form:     (x - a)2 + (y - b)2 + (z - c)2 = r2
(x − )2 + (y − )2 + (z − )2 = 2
Sphere form:     x2 + y2 + z2 + Ax + By + Cz + D = 0
x2 + y2 + z2 + x + y + z + = 0
NOTES:
d   (distance spheres centers)
α   (alfa)
θ   (teta)
h   (intersection circle radius)
intersection plane equation
intersection circle center
Spheres lapping volume
Spheres caps volume
Spheres volume
Spheres center parametric line

Two spheres intersection summary

Print two spheres summary
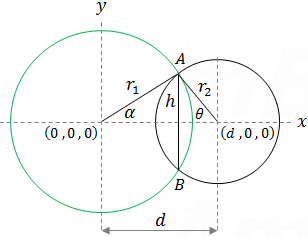
Two spheres drawing The equations of the spheres are given by:
(x − x1)2 + (y − y1)2 + (z − z1)2 = r12             (1)
(x − x2)2 + (y − y2)2 + (z − z2)2 = r22             (2)
The outer intersection points of the two spheres forms a circle (AB) with radius   h   which is the base of two spherical caps.
To make calculations easier we choose the center of the first sphere at (0 , 0 , 0) and the second sphere
at (d , 0 , 0).
The distance   d   between the spheres centers is:
Distance d
Now we can find the angle  α  and   θ   by the cosine law:
Distance d Distance d
Once we found the angle α  we can find the intersection circle radius  h.
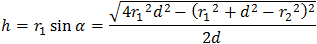Intersection circle radius
The lapping volume between the two spheres contains two spherical caps the height of the spherical cap can be found by the same way as circular segment height.
The height of the spherical cap 1 is: h1 = r1 * (1 − cos α)
The height of the spherical cap 2 is: h2 = r2 * (1 − cos θ)
NOTE: when   α   or   θ   is bigger then 90 degrees then the spherical cap height is more then the radius and the volume of the cap is more then half sphere.
The volume of the lapping area which contains the two spherical caps is:
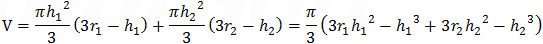
Lapping volume
The equation of a sphere can be described by the equation:         x2 + y2 + z2 + Ax + By + Cz + D = 0
The connections of the coefficients A, B, C and D to eq. (1) are:
A1 = − 2x1 B1 = − 2y1 C1 = − 2y1 D1 = x12 + y12 + z12 − r12
If both spheres are given in this form the distance  d  between spheres centers is:
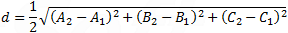Distance between spheres centers
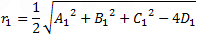Sphere 1 radius is:          Radius of first sphere
If we subtract the two spheres equations from each other we receive the equation of the plane that passes through the intersection points of the two spheres and contains the circle AB.
X 2(x2 − x1) + Y 2(y2 − y1) + Z 2(z2 − z1) + x12 − x22 + y12 − y22 + z12 − z22 − r12 + r22 = 0             (3)
General plane equation is: XA + YB + ZC + D = 0 where:
A = 2(x2 − x1) B = 2(y2 − y1) C = 2(z2 − z1) D = x12 − x22 + y12 − y22 + z12 − z22 − r12 + r22
The equation of the line that connects the sphere’s centers is by parametric line equation
x = x1 + t(x2 −x1) y = y1 + t(y2 −y1) z = z1 + t(z2 −z1) (4)
The center point of circle AB is located at the point of intersection of the parametric line connecting the spheres centers eq. (4) and the plane of the spheres intersection eq. (3) which also contains the circle AB.
By substituting eq. (4) into eq. (3) we can find the value of   t   which is:
(x1 + t x2 − t x1)A + (y1 + t y2 − t y1)B + (z1 + t z2 − t z1)C + D = 0
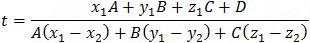Value of parameter t
Substitute the value of  t  into eq. (4) to get the coordinate of the intersection circle (AB) center.
The type of intersection of two spheres depends on the size of the radii and the distance between the sphere’s centers.
Description Result
d < r1 + r2
d > |r1 − r2|		 Conditions for intersection
d > r1 + r2 Two separate spheres
d = r1 + r2 Outer tangency
d < |r1 − r2| One sphere inside the other
d = |r1 − r2| inner tangency