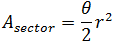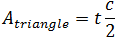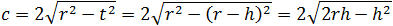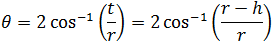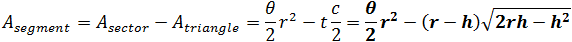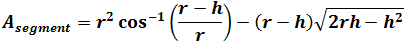☖ Home ⇄ Units Converter ⧉ Geometry Σ Math ✈ Physics 〶 Electricity
Circle Arc, segment, sector Torus Example 1-Sigment

Circle calculator

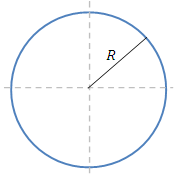
circle
Circle

* Input a value in any field

Radius (R)
Diameter (D)
Circumference (P)
Area (A)
Circle equations summary

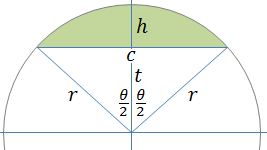
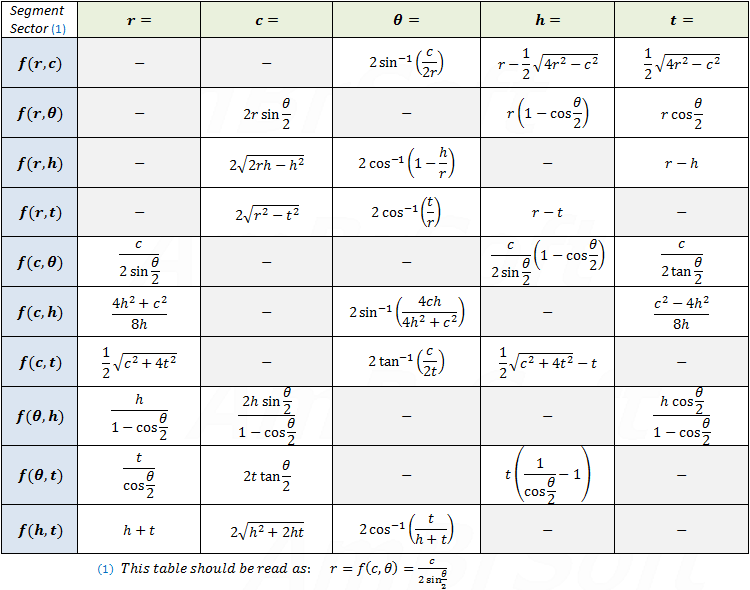
Arc, Segment, Sector Calculator and equations

Arc
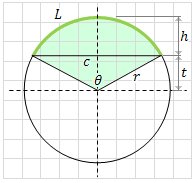
Arc, Segment and Sector

* Input 2 values in any unmarked fields

   
Input limit:
Radius (r)
Central angle (θ)
Arc length (L)
Sector area
Sector circumference
Segment area
Segment circumference
Triangle base (c)
Segment height (h)
Triangle height (t)

Arc, segment and sector equations summary

Arc, segment and sector equations summary

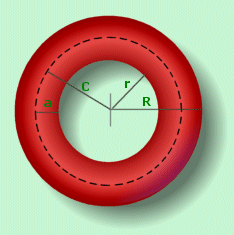
Torus calculator and equations

Torus

Torus

* Input 2 values in any unmarked field

Input limit:
Outer radius (R)
Inner radius (r)
Ring radius (a)
Mean radius (c)
Torus volume (V)
Torus surface Area (S)
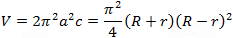
Torus volume

S = 4π2a c = π2(R + r)(R − r) = π2(R2 − r2)

R = c + a                             r = c − a

Torus geometry

Example 1 - segment area Print line equations ▲
Find the expression for the area of a segment defined by the radius  r  and the segment height  h.
Segment example
The area of a sector whose angle equals to θ is:
A_sector=θ/2 r^2 (θ in radians)
The area of the triangle formed by the two radii and
the cord  c  is: A_triangle=t c/2
The value of  t  is: t = r - h
The value of  c  using the Pythagoras theorem is:
c=2√(r^2-t^2 )=2√(r^2-(r-h)^2 )=2√(2rh-h^2 )
θ is: θ=2 cos^(-1)⁡(t/r)=2 cos^(-1)⁡((r-h)/r)
Now the area of the segment is:
A_segment=A_sector-A_triangle=θ/2 r^2-t c/2=θ/2 r^2-(r-h) √(2rh-h^2 )
And after substituting the value of  θ  we get the final value:
A_segment=r^2 〖cos〗^(-1)⁡((r-h)/r)-(r-h) √(2rh-h^2 )
Notice that when   r = h   (segment is half circle)   Asegment = r2cos-1 0 = r2 π / 2   this is half circle area.