Plane and line intersection

Intersection of a Plane and a line calculator

Parametric line equation	L₁	x =	+	t
		y =	+	t
		z =	+	t

Classic line equation

L₁

x +

y +

z +

Line defined by 2 points	L₁	x₁		y₁		z₁
Line defined by 2 points	L₁	x₂		y₂		z₂

Line defined by vector	L₁	Vector: i + j + k
		Point: x: y: z:

Plane in three dimensional coordinates Ax + By + Cz + D = 0

Plane equation:

x + y + z + = 0

Plane passing through 3 points:

x_a

y_a

z_a

x_b

y_b

z_b

x_c

y_c

z_c

Plane and line intersection point:

Angle between plane and line:

Intersection of plane and line summary

Plane and line intersection

Plane:	Ax + By + Cz + D = 0
Line:	x = x₁ + at
	y = y₁ + bt
	z = z₁ + ct

Note if the line is given by a vector
ai + bj + ck and a point (x_p , y_p , z_p), We can translate it to parametric form by the equations:

x = x_p + at

y = y_p + bt

z = z_p + ct

To find the intersection point P(x,y,z), substitute line parametric values of x, y and z into the plane equation:

A(x₁ + at) + B(y₁ + bt) + C(z₁ + ct) + D = 0

and valuating t gives:

To find intersection coordinate substitute the value of t into the line equations:

x=x_1-a(Ax_1+By_1+cz_1+D)/(Aa+Bb+Cc) y=y_1-b(Ax_1+By_1+cz_1+D)/(Aa+Bb+Cc) z=z_1-c(Ax_1+By_1+cz_1+D)/(Aa+Bb+Cc)

Angle between the plane and the line:

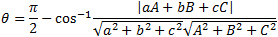
Angle between plane and a line

Note: The angle is found by dot product of the plane vector and the line vector, the result is the angle between the line and the line perpendicular to the plane and θ is the complementary to π/2.

A line will be parallel to the plane if: aA + bB + cC = 0

Intersection of plane and line example

Find the intersection point and the angle between the planes: 4x + z − 2 = 0 and the line

given in parametric form: x =− 1 − 2t y = 5 z = 1 + t

Because the intersection point is common to the line and plane, we can substitute the line parametric points into the plane equation to get:

4(− 1 − 2t) + (1 + t) − 2 = 0

t = − 5/7 = 0.71

Now we can substitute the value of t into the line parametric equation to get the intersection point.

x = − 1 − 2(− 5/7) = 3/7 = 0.43

y = 5

z = 1 − 5/7 = 2/7 = 0.29

And the intersection point is: (0.43 , 5 , 0.29).

The angle between the line and the plane can be calculated by the cross product of the line vector with the vector representation of the plane which is perpendicular to the plane: v = 4i + k

The line vector representation is the t portion of the parametric line equation: n = -2i + k

And the angle between the plane and the line is: θ = π/2 − α = π/2 − 40.6 = 49.4 degree