☖ Home ⇄ Units Converter ⧉ Geometry Σ Math ✈ Physics 〶 Electricity

Hyperbola with center at (x1 , y1) calculator

Print hyperbola calculator
(x − )2  −  ( y − )2  = 1
2 2
x2 − y2 + x + y + = 0
hyperbola figure - 1
Transverse axis length (a)
Conjugate axis length (b)
Foci distance (c)
Eccentricity (e)
Center of hyperbola
Foci coordinates
Vertex coordinates
Coordinates of (b)
Asymptotes line
Latus rectum length
Point x1
Point y1
Tangent line at (x1 , y1)
Tangent line at (x2 , y2)
Input limit:
Notes:
Hyperbola equation:
              
Intersecting line equation     ay = mx + c
y = x +
Intersection: Point 1
Point 2
Hyperbola center (0,0) summary Eq. verification ex: 1 , 1a , 1b Center and foci ex: 5
Hyperbola and line intersection Tangent line ex: 2 , 2a , 2b Hyperbola equation ex: 6
Hyperbola center (h,k) summary Eccentricity ex: 3 , 3a Converting formats ex: 7
Hyperbola and line intersection Foci ex: 4 , 4a , 4b Hyperbola and line ex: 8
Hyperbola - with center at  (0 , 0)  summary Print hyperbola summary ▲
hyperbola figure - 1
A hyperbola is the locus of all points the difference of whose distances from two fixed points
is a positive constant |d1 - d2| = constant.
the two fixed points are called the foci.
The general equation of a hyperbola is:
distance between both foci is:   2c
a and b − major and minor radius
General equation of a hyperbola is: Hyperbola general equation (center at   x = 0   y = 0)
The line through the foci  F1  and  F2  of a hyperbola is called the transverse axis and the perpendicular bisector of the segment  F1  and  F2  is called the conjugate axis the intersection of these axes is called the center of the hyperbola.
The eccentricity  e  of a hyperbola is: Eccentricity
Where   (c = half distance between foci)         c > a           then always           e > 1
The vertices of a hyperbola are the intersection points of the transverse axis and the hyperbola.
hyperbola figure - 1
From hyperbola definition   |d1 − d2| = const
And from x direction      2c + 2(a − c) = const
2d = 2a
And we get the relation   d = a   and:
b=√(c^2-a^2 )
The points  A1  and  A2  in this case  (±a , 0)  are the vertices of the transverse axis.
The two distinctive tangent lines shown as dashed lines are called the asymptotes and has the equations:
y=b/a x and y=-b/a x
hyperbola figure - 1
Any hyperbola has 3 distinctive regions:
Region Relation Condition Notes
① y=b/a x   −
② y=b/a x x > a Tangent line to the hyperbola exists only in this region (blue).
③ y=b/a x x < −a −
Horizontal and vertical hyperbolas with center at (0 , 0) summary table
Hyperbola
center at (0 , 0)		 Horizontal Vertical                       Print summary table
Hyperbola equation Horizontal hyperbola Vertical hyperbola
b2x2 − a2y2 − a2b2 = 0
or        Ax2 − By2 + C = 0		 −a2x2 + b2y2 − a2b2 = 0
or        Ay2 − Bx2 + C = 0
Hyperbola direction left - right   (horizontal) up - down     (vertical)
Vertices coordinates (a) (−a , 0)  and  (a , 0) (0 , −a)  and  (0 , a)
Foci coordinates (c) (−c , 0)  and  (c , 0) (0 , −c)  and  (0 , c)
Conjugate (b) (0 −b)  and  (0 , b) (−b , 0)  and  (b , 0)
Asymptote’s line y=±b/a x y=±a/b x
Slope at (x0 , y0) any
point on the hyperbola
 dy/dx=m=(b^2 x_0)/(a^2 y_0 ) dy/dx=m=(a^2 x_0)/(b^2 y_0 )
x0 is given   ⟶   y0 is: y_0=±b/a √(〖x_0〗^2-a^2 ) y_0=±a/b √(〖x_0〗^2+b^2 )
y0 is given   ⟶   x0 is: x_0=±a/b √(〖y_0〗^2-b^2 ) x_0=±b/a √(〖y_0〗^2-a^2 )
Converting hyperbola presentation formats:   (See detail calculation)
①                 Ax2 + By2 + E = 0
② Hyperbola with center at (0 , 0)
① → ② a=√((-E)/A) b=√((-E)/B)
If    E < 0 Horizontal
If    E > 0 Vertical
If    E = 0 Not hyperbola
② → ① A = b2 B = −a2 E = − a2b2
③ Hyperbola with center at (0 , 0)
③ → ① A = −a2 B = b2 E = − a2b2
Latus rectum
The line passing through the focus of the hyperbola and is perpendicular to the transverse axis starting from one side of the hyperbola to the opposite side is called the latus rectum (L) and is equal to:
L=(2b^2)/a
The height  y0  from the hyperbola equation is:
y_0=2 b/a √(〖x_0〗^2-a^2 )=2 b/a √(c^2-a^2 )=(2b^2)/a
Hyperbola - with center at  (h , k)  summary Print hyperbola center at (h,k) summary ▲
hyperbola with center at (h,k)
If the center of the vertical horizontal is moved by the values     x = h   and   y = k   (positive directions) then the equation of the hyperbola becomes:
(x-h)^2/a^2 -(y-k)^2/b^2 =1horizontal
The location of the vertices, foci and b are presented in the drawings at left.
hyperbola with center at (h,k)
If the center of the vertical hyperbola is moved by the values     x = h   and   y = k   (positive axis directions) then the equations of the hyperbola becomes:
(y-k)^2/a^2 -(x-h)^2/b^2 =1vertical
We can see that the y and x values swap places and now the x variable is the negative.
In order to make the solution of shifted hyperbola easier we can perform a transformation T that will center the hyperbola to the origin and after all the calculations we can transform the answers back to the real values.
T = (h , k) and back by the same transformation T = (h , k) (See example 3a)
Horizontal and vertical hyperbolas with center at (h , k) summary table
Hyperbola
center at (h , k)		 Horizontal Vertical                       Print summary table
Hyperbola equation (x-h)^2/a^2 -(y-k)^2/b^2 =1 (y-k)^2/a^2 -(x-h)^2/b^2 =1
Ax2 − By2+ Cx + Dy + E = 0 Ay2 − Bx2 + Cx + Dy + E = 0
Hyperbola direction left - right    (horizontal) up - down     (vertical)
Vertices (a) (h − a , k)  and  (h + a , k) (h , k − a)  and  (h , k + a)
Foci location (c) (h − c , k)  and  (h + c , k) (h , k − c)  and  (h , k + c)
Conjugate (b) (h , k − b)  and  (h , k + b) (h − b , k)  and  (h + b , k)
Asymptote’s line y=k±b/a (x-h) y=k±a/b (x-h)
Slope at (x0 , y0) any
point on the hyperbola
 dy/dx=(b^2 x_0-hb^2)/(a^2 y_0-ka^2 ) dy/dx=(a^2 x_0-ha^2)/(b^2 y_0-kb^2 )
x0 is given   ⟶   y0 is: x_0=a/b √((y_0-k)^2+b^2 )+h y_0=k±a/b √((x_0-h)^2+b^2 )
y0 is given   ⟶   x0 is: x_0=a/b √((y_0-k)^2+b^2 )+h x_0=a/b √((y_0-k)^2+b^2 )+h
Converting hyperbola presentation formats:   (See calculation example)
Table-1
Intersection of hyperbola with center at  (0 , 0)  and line    y = mx + c Print hyperbola summary ▲
hyperbola line intersection figure - 1 hyperbola line intersection figure - 2
Parameter Horizontal Vertical
Hyperbola x^2/a^2 -y^2/b^2 =1 y^2/a^2 -x^2/b^2 =1
x coordinate x_1,2=(b^2 mc±ab√(〖b^2 m〗^2+c^2-a^2 ))/(〖b^2 m〗^2-a^2 ) x_1,2=(a^2 mc±ab√(c^2+b^2-a^2 m^2 ))/(b^2-a^2 m^2 )
y coordinate y1,2 = mx1,2 + c
2 points c2 > a2m2 − b2 c2 > a2 − b2m2
1 point c2 = a2m2 − b2 c2 = a2 − b2m2
No intersection c2 < a2m2 − b2 c2 < a2 − b2m2
Intersection of hyperbola with center at  (h , k)  and line    y = mx + c Print hyperbola summary ▲
hyperbola line intersection figure - 1 hyperbola line intersection figure - 2
Parameter Horizontal Vertical
Hyperbola (x-h)^2/a^2 -(y-k)^2/b^2 =1 (y-k)^2/a^2 -(x-h)^2/b^2 =1
x coordinates
   Horizontal
    φ = c − k		 x_1,2=(-hb^2-mφa^2±ab√(2hmφ+m^2 h^2+b^2 m^2+φ^2-a^2 ))/(b^2-m^2 a^2 )
x coordinates
   Vertical
    φ = c − k		 x_1,2=(-ha^2-mφb^2±ab√(2mφh+m^2 h^2+b^2 m^2+φ^2-a^2 ))/(b^2 m^2-a^2 )
y coordinates y1,2 = mx1,2 + c
2 points b2 < a2 m2 − (mh + φ)2 a2 < (mh + φ)2 + b2 m2
1 point b2 = a2 m2 − (mh + φ)2 a2 = (mh + φ)2 + b2 m2
No intersection b2 > a2 m2 − (mh + φ)2 a2 > (mh + φ)2 + b2 m2
Example 1 - Verify the equation of a hyperbola Print example 1 - of the hyperbola equation ▲
hyperbola figure - 1
From the definition of the hyperbola, we know that:
d2 − d1 = ±2a
Where  a  is equal to the x axis value or half the transverse axis length.
From the drawing d1 and d2 are equal to:
d1 and d2
√((x-c)^2+y^2 )-√((x+c)^2+y^2 )=±2a
Simplify the equation by transferring one radical to the right and squaring both sides:
√((x-c)^2+y^2 )=±2a+√((x+c)^2+y^2 )
After rearranging terms, we obtain: a+c/a x=±√((x+c)^2+y^2 )
We square again both sides to find: a^2+2cx+c^2/a^2 x^2=(x+c)^2+y^2
After arranging terms, we get: (c^2/a^2 -1) x^2-y^2=c^2-a^2
Dividing by   a2 − c2   we find: x^2/a^2 -y^2/(c^2-a^2 )=1
Since   b2 = c2 − a2   we get the general equation of the hyperbola.
hyperbola figure - 1
If the foci are placed on the  y  axis then we can find the equation of the hyperbola the same way:   d2 − d1 = ±2a
Where  a  is equal to the half value of the conjugate axis length.
From the drawing d1 and d2 are equal to:
d_2=√((x-0)^2+(y+c)^2 )=√(x^2+(y+c)^2 )
d_1=√((x-0)^2+(y-c)^2 )=√(x^2+(y-c)^2 )
Substitute values into d1 and d2 we get:
√(x^2+(y-c)^2 )-√(x^2+(y+c)^2 )=±2a
After arranging terms and square both sides we get:
x^2+(y-c)^2=x^2+(y+c)^2+4a^2±4a√(x^2+(y+c)^2 )
After cancelling terms, we find: ((c^2-a^2)/a^2 ) y^2-x^2=c^2-a^2
After dividing by  b2  we get the final form: Vertical hyperbola equation
Example 1a - Verify the equation of a hyperbola Print example 1a - of the hyperbola equation ▲
Verify why the equation   y2 − 36x2 − 72x − 12y = 0   is not a hyperbola.
By the method of completing the square formula we have:
(y2 − 12y) − (36x2 + 72x) = 0
(y2 − 12y) − 36(x2 + 2x) = 0
[(y − 6)2 − 36] − 36[(x + 1)2 − 1] = 0
(y − 6)2 − 36 − 36(x + 1)2 + 36 = 0
(y − 6)2 − 36(x + 1)2 = 0
Calculate  a2  and  b2   we get: a^2=φ/A=0 b^2=φ/B=0
For hyperbola  a  and  b  cannot be equal to zero.
Example 1a draw
We can further investigate the given equation and find the intercepts with the y axis by setting x = 0
y2 − 12y = 0
y(y − 12) = 0
The solutions are   y = 0   and   y = 12
Applying the same process to find the x axis intercepts where   y = 0
36x2 + 72x = 0
x(36x + 72) = 0
The solutions are   x = 0   and   x = −2
From the equation   (y − 6)2 − 36(x + 1)2 = 0   we can see that when
y = 6   and   x = −1   the left side is equal to 0 and hence a solution.
The result is a double line with same slope one positive and the other negative, the lines intersects at   (−1 , 6)   see sketch at left.
Example 1b - Direction and basic values of a hyperbola Print example 1a - of the hyperbola equation ▲
Find the direction, vertices and foci coordinates of the hyperbola given by   y2 − 4x2 + 6 = 0.
transfer  6  to the other side of the equation we get: y2 − 4x2 = −6
Divide both sides by  −6 y^2/(-6)-(4x^2)/(-6)=1
After arranging numbers x^2/1.5-y^2/6=1
From the hyperbola equation we see that the coefficient of  x2  is positive and of  y2  is negative so the hyperbola is horizontal with the values         h = 0 ,         k = 0         a2 = 1.5         b2 = 6
The center is located at: (0 , 0)
The coordinates of the vertices are: (-√1.5 ,0) ( √1.5 ,0)
(−1.22 , 0)       (1.22 , 0)
The values of the foci are: c=√(a^2+b^2 )=√(1.5+6)=√7.5=2.74
The coordinates of the foci are: (−2.74 , 0)       (2.74 , 0)
The eccentricity is: e=c/a=2.74/√1.5=2.24
or e=√(a^2+b^2 )/a=√(1+b^2/a^2 )=√(1+4)=√5
Example 2 - Tangent line to hyperbola Print exampe of tangent line to a hyperbola ▲
Find the equation of the line tangent to the hyperbola   x2 − 4y2 − 16 = 0   at the point   P0(5 , 1.5).
By implicit differentiation we will find the value of   dy/dx   that is the slope at any  x and y  point.
Implicit differentiation   dy/dx   is: Implicit differentiation
The value of dy/dx is: Vertical hyperbola
At the given point the slope is: hyperbola tangent slope
Equation of the tangent line that passes through the given point P0 on the hyperbola and has slope m is
Vertical hyperbola
given by the equation:       y = mx + (yp − mxp)
Substitute the point P0(5 , 1.5) we get:
y = mx + (1.5 − m * 5)
And the tangent line equation is:     5x − 6y − 16 = 0
(see the sketch of the tangent line at left)
It can be seen that the point  x0  on the  x  axis must be located in the region     |x0| > a       or
x0 < − 4    and    P0 > 4
Example 2a - Tangent line to hyperbola passing through a point Print exampe of tangent line to an hyperbola ▲
Given the hyperbola Exercise 2a Find the equation of the lines tangent to this hyperbola and
passing through the point (1 , −1).
By implicit differentiation we will find the value of   dy/dx   that is the slope at any  x and y  point.
2x/a^2 -2y/b^2 dy/dx=0 → dy/dx=2x/a^2 b^2/2y=b^2/a^2 x/y=m
Ex 2a hyperbola
Slope at point (x0 , y0) is m=x_0/(3y_0 )
(1)
The tangent line L1 is tangent to the hyperbola at (x0 , y0) hence it satisfies the hyperbola equation:
〖x_0〗^2/6-〖y_0〗^2/2=1 (2)
Now the equation of the line passing through the point (x1 , y1) and has a slope of m is:
y = mx + y1 − m x1
The point (x0 , y0) is located on the line hence it satisfies the equation of the line.
y0 = mx0 + y1 − m x1 (3)
After substituting the values of x1 = 1 and y1 = −1 in equation 3. we should solve the three equations
(1) (2) and (3) which has three unknowns x0, y0 and m.
From equation (2) we have x02 − 3 y02 − 6 = 0 (2)
Inserting (1) to (3) and multiplying by 3y0 x02 − 3 y02 − 3y0 − x0 = 0 (4)
Inserting from equation (2) the value x02 − 3 y02 = 6 into equation (4) we get
x0 = 6 − 3y0 (5)
Inserting equation (5) into equation (2) we get: (6-3y_0 )^2/6-〖y_0〗^2/2=1
And finally, we get the quadratic equation: y02 − 6y0 + 5 = 0
And the solution is: y_0=(6±√(36-20))/2=5 ,-1
From equation (5) we find the x values: x0 = 6 − 3 * 5 = −9 and x0 = 6 − 3 * 1 = 3
The tangency points are:   (−9 , 5)   and   (3 , 1)
The tangent lines equation can be found by: (y-y_1)/(y_2-y_1 )=(x-x_1)/(x_2-x_1 )
And we find the 2 tangent lines to be: L1:   3x + 5y + 2 = 0 L2:   x − y − 2 = 0
If we solve the general case of tangency from any point, we get the following equations:
y_0,2=(-a^2 b^2 y_1±bx_1 √(a^2 b^2+a^2 〖y_1〗^2-〖x_1〗^2 ))/(a^2 〖y_1〗^2-〖x_1〗^2 )
x_0=(a^2 b^2+a^2 y_1 y_0)/(b^2 x_1 )
Example 2b - Asymptotes and conjugate axis Print exampe of tangent line to an hyperbola ▲
The conjugate axis length of a hyperbola with center at (0 , 0) is equal to  8  and the asymptotes
are  y = ±2x.  Find the equation of the hyperbola.
Hyperbola of example 2b
From the conjugate length we can find the value of   b.
2b = 8       and   b = 4
From the slope of the asymptotes, we can find the value of the transverse axis length   a.
b / a = ±2
a = b / 2 = 4 / 2 = 2
x^2/1-y^2/4=1
4x2 − y2 − 16 = 0
Example 3 - vertices and eccentricity Print vertices and eccentricity example ▲
Find the equation of the hyperbola with vertices at  (0 , ± 6)  and eccentricity of 5 / 3.
Notice that the vertices are on the  y  axis so the equation of the hyperbola is of the form. y^2/a^2 -x^2/b^2 =1
The value of the vertices from the given data is:  6  along the  y  axis.
Since the eccentricity is:    e = c / a c = e * a = 5 * 6 / 3 = 10
The co vertices in the x direction is: b=√(c^2-a^2 )=√(100-36)=8
The equation of the hyperbola is: y^2/6^2 -x^2/8^2 =1
The foci are at the points: (0 , 10)     and     (0 , −10)
Latus rectum coordinate is the value   x0   of the graph at the point y0 = c = 10
y_0=(±b√(〖x_0〗^2-a^2 ))/a=(±b√(c^2-a^2 ))/a=(±8√(100-36))/6=±32/3
And the latus rectum length is: L = 2 * x0 = 2 * 10.67 = 21.33
The latus rectum is also equal to   L = 2 * b2 / a
Example 3a - vertices and eccentricity Print vertices and eccentricity example ▲
Find the vertices, foci and  b  lengths and the coordinates of the hyperbola given by the equation:
(y-4)^2/9-(x+2)^2/16=1 (Use the center transformation to the origin).
Because the sign of  x  is negative then the foci and the vertices are located on the  y  axis.
Hyperbola center shift From the hyperbola equation we can see that in order to move the center to the origin we have to subtract 2 in the x direction and add 4 in the y direction that is the transformation Tx,y(−2 , 4).
(y-4+T_y )^2/9-(x+2-T_x )^2/16=1
and we get the equation: y^2/9-x^2/16=1
From the hyperbola equation we can see that    a2 = 9    a = 3    and    b2 = 16    b = 4.
The distance of the foci is: c=√(a^2+b^2 )=√(3^2+4^2 )=±5
The eccentricity of the hyperbola is: e=c/a=5/4=1.25
The coordinates of the vertices are: (0 , −3)       and       (0 , 3)
The coordinates of the foci are: (0 , −5)       and       (0 , 5)
The coordinate of b in x direction: (−4 , 0)       and       (4 , 0)
Now we have to transform back the values of the coordinates by the value:  T −1 = (−2 , 4)  this transformation values are the same as  Tx,y  that is because the values of  h  and  k  in the hyperbola are actually at the opposite sign values for example the value  (x − 2)  means a point at  x = +2.
The coordinates of the vertices are: (0 − 2 , −3 + 4)  ,  (0 − 2 , 3 + 4)        →      (−2 , 1) , (−2 , 7)
The coordinates of the foci are: (0 − 2 , −5 + 4)  ,  (0 − 2 , 5 + 4)        →      (−2 , −1) , (−2 , 9)
The coordinates of b in x direction: (−4 − 2 , 0 + 4)  ,  (4 − 2 , 0 + 4)        →      (−6 , 4) , (2 , 4)
Example 4 - foci and eccentricity Print example foci and e ccentricity ▲
Find the equation of the hyperbola that has eccentricity of  1.5,  and foci at points  (±6 , 0).
We see that the foci are located on the transverse axis   (x axis)   so the hyperbola is horizontal.
The value of the vertex is: a=c/e=6/1.5=4
The value of   conjugate axis length b   is: b=√(c^2-a^2 )=√(36-16)=√20
And the equation of the hyperbola is: x^2/25-y^2/31.25=1
Example 4a - eccentricity and a point Print example foci and e ccentricity ▲
Find the equation of the hyperbola that has eccentricity of  2.236,  and center at origin, passing through the point  (3 , 2).
The given point is located on the hyperbola hence it fulfills the equation of the hyperbola
Point   (x1 , y1) 〖x_1〗^2/a^2 -〖y_1〗^2/b^2 =1 (1)
From the equation: e=c/a=√(a^2+b^2 )/a=√(1+b^2/a^2 )
We have: b2 = a2(e2 − 1) (2)
Substitute  (2)  into  (1): 〖x_1〗^2/a^2 -〖y_1〗^2/(a^2 (e^2-1) )=1 (3)
Solving for  a  we get: x12(e2 − 1) − y12 − a2(e2 − 1) = 0
And the value of  a  is: a^2=〖x_1〗^2-〖x_1〗^2/(e^2-1)=〖x_1〗^2 (1-1/(e^2-1)) (4)
Substitute point  (3 , 2)  to equation (4) to get  a2: a^2=9-4/(5-1)=8
Substitute point  a  to equation (2) to get  b2 b2 = 8(5 − 1) = 32
And the equation of the hyperbola is: 4x2 − y2 − 32 = 0
Example 4b - foci and a point Print example foci and e ccentricity ▲
Find the equation of the hyperbola that has foci at  (0 , ±4),  and center at origin, passing through the point  (1 , 3).
The foci points are located on the  y  axis hence the hyperbola is a vertical.
The given point is located on the hyperbola so they fulfill the hyperbola equation.
Point   (x1 , y1) 〖y_1〗^2/a^2 -〖x_1〗^2/b^2 =1 (1)
From the equation: c2 = a2 + b2
We have: b2 = c2 − a2 (2)
Substitute  (2)  into  (1): 〖x_1〗^2/a^2 -〖y_1〗^2/((c^2-a^2 ) )=1 (3)
Solving for  a  we get: a4 − a2(c2 + x12 + y12) + c2y12 = 0
Set u = a2 we get a quadratic equation with  u:           u2 − u(c2 + x12 + y12) + c2y12 = 0
The solution is: u_1,2=1/2 √((c^2+〖x_1〗^2+〖y_1〗^2 )^2+4c^2 〖x_1〗^2 )
(4)
And the value of  a2  is: a2 = u
The value of   b   can be found by equation  (2).
Substitute point  (2 , 3)  to equation (4) to get: u=(23±√(〖23〗^2-4∙10∙3^2 ))/2=18 ,5
The focus should be bigger then  a  so a2 is: a2 = u = 8
The value of  b2 is: b2 = c2 − a2 = 16 − 8 = 8
And the equation of the hyperbola is: y2 − x2 = 8
Example 5 - Center of hyperbola Print example 5 center and foci of hyperbola ▲
Find the center the foci and the vertices coordinate of the hyperbola given by the equation
x2 − 16y2 − 4x − 32y − 28 = 0.  analyse the case that the last term is  +28
Divide terms into x and y variables: (x2 − 4x       ) − (16y2 + 32y       ) − 28 = 0
By applying the method of completing the square formula     (x + a)2 = x2 + 2ax + a2     we get:
(x − 2)2 − 4 − 16(y + 1)2 + 16 − 28 = 0
(x − 2)2 − 16(y + 1)2 = 16
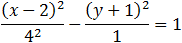After dividing by 16 we get: (x-2)^2/4^2 -(y+1)^2/1=1
The center of this hyperbola is at    (2 , − 1)        h = −2   and   k = 1.
The transvers axis half length  (a)  is equal to 4.
and the conjugate axis half length  (b)  is equal to 1.
Because   a > b   this hyperbola is horizontal so the transverse axis is along the  x  axis.
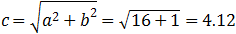The foci distance is calculated from the equation: c=√(a^2+b^2 )=√(16+1)=4.12
In order to find the coordinates of the foci we will take the center of the hyperbola at (2 , −1) and add and subtract the value of c in the x direction.
(2 + c , −1)   (2 − c , −1)      =      (2 + 4.12 , −1)   (2 − 4.12 , −1)         =         (6.12 , −1)   (−2.12 , −1)
To find the coordinate of the vertices we perform the same process as for the foci but with the value of a.
(2 + a , −1)   (2 − a , −1)      =      (2 + 4 , −1)   (2 − 4 , −1)         =         (6 , −1)   (−2 , −1)
Repeat the same method as before but with + sign instead of minus   x2 − 16y2 − 4x − 32y + 28 = 0
(x2 − 4x       ) − (16y2 + 32y       ) + 28 = 0
(x − 2)2 − 4 − 16(y + 1)2 + 16 + 28 = 0
(x − 2)2 − 16(y + 1)2 = −40
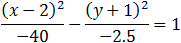Divide by −40 and again by 16 we get: (x-2)^2/(-40)-(y+1)^2/(-2.5)=1
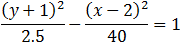and finally, (y+1)^2/2.5-(x-2)^2/40=1
We can see that changing the sign of the last term changed the value of the free term to negative and hence the hyperbola changed to vertical also the values of  a  and  b  had been changed.
Example 6 - Equation of hyperbola Print example -6 hyperbola equation ▲
Find the equation of the locus of all points the difference of whose distances from the fixed points   (0, 2)   and   (0, 10)   is  6.
The fixed points are the foci of the hyperbola and they are located on the  y  axis so the transverse axis of the hyperbola is on the  y  axis and the hyperbola is vertical.
The focus is equal to: c=√((x_2-x_1 )^2+(y_2-y_1 )^2 )/2=√((0-0)^2+(10-2)^2 )/2=4
From the definition of the hyperbola, we know that: d2 − d1 = 2a
and the value of  a  is     6 = 2a a = 6 / 2 = 3
and the value of conjugate vertex   b   is: Foci distance
The hyperbola in the   x'y'   (0,0)   system is: y^2/9-x^2/5=1
From the two points of the foci the center of the hyperbola can be found at:
Hyperbula center at (0 , 6)
We can see that the hyperbola is moved upward from the origin by the value  k = 6  hence the hyperbola equation turns to be:
(y-6)^2/9-x^2/5=1
Or by multiplying terms we get the form: −9x2 + 5y2 − 60y + 135 = 0
Example 7 - Converting hyperbola formats Print example converting hyperbola formats ▲
Find the translation equations between the two forms of hyperbola.
① Ax2 − By2 + Cx + Dy + E = 0 ② Hyperbola general equation
From equation ② we have: b2 (x + h)2 − a2 ( y + k)2 = a2b2
b2 (x2 + 2hx + h2) − a2(y2 + 2ky + k2) = a2b2
And finally: b2 x2 + 2b2hx + b2h2 − a2y2 − 2a2ky − a2k2 − a2b2 = 0
Rearranging by powers order: b2 x2 − a2 y2 + 2b2h x − 2a2k y + b2h2 − a2k2 − a2b2 = 0
Now we can find the values of the coefficients of the hyperbola equation   ①   A, B, C, D and E.
A = b2 B = −a2 C = 2b2h D = −2a2k E = b2h2 − a2k2 − a2b2
For example: (x-2)^2/4-(y+1)^2/2=1 → 2x2 −4y2 − 8x − 8y − 4 = 0
A = 2 B = −4 C = 2∙2∙(−2) = −8 D = −2∙4∙1 = −8 E = 8 −4 −8 = −4
The transformation from equation ① to equation ② includes more steps to solve:
From equation ① we have: (A x2 + C x) − (B y2 − D y) = −E
Take A and B out of both parenthesis: Hyperbola power order equation
Now use the square identities to get the square equations:
(x-C/2A)^2=x^2-C/A x+C^2/〖4A〗^2 (y-D/2B)^2=y^2-D/B y+D^2/〖4B〗^2
We have to remember to subtract the bold square complements values from the square equation:
A(x-C/2A)^2-C^2/4A-B(y-D/2B)^2+D^2/4B=-E
A(x-C/2A)^2-B(y-D/2B)^2=C^2/4A-D^2/4B-E
(x-C/2A)^2/B-(y-D/2B)^2/A=C^2/(4A^2 B)-D^2/(4AB^2 )-E/AB
Let  φ  be equal to the right side of the equation: φ=C^2/(4A^2 B)-+D^2/(4AB^2 )-E/AB
Divide both sides by the value of  φ  to get the standard form: (x-C/2A)^2/Bφ-(y-D/2B)^2/Aφ=1
h=-C/2A k=-D/2B a^2=Bφ b^2=Aφ
For example: x2 −10y2 + 4x + 20y − 16 = 0 → h=-C/2A k=-D/2B a^2=Bφ b^2=Aφ
Example - 8 hyperbola and line intersection Print example - 8 hyperbola and line intersection ▲
Find the intersection points of the hyperbola given by the equation      Hyperbola ex - 8
and the line     y= −2x + 6.     Suppose that   h = 2   k = −4   a = 2  and  b = 6
From the hyperbola equation b2 (x − h)2 − a2 (y − k)2 = a2 b2
Insert  y  value from the line equation b2 (x2 − 2xh + h2) − a2 (mx + c − k)2 − a2 b2 = 0
Mark:       c − k = φ
Open parenthesis b2x2 − 2xhb2 + b2h2 − a2m2x2 − 2mxφa2 − a2φ2 − a2b2 = 0
Arrange by powers (b2 − m2 a)2 x2 − (2hb2 + 2mφa2) x + b2h2 − a2φ2 − a2b2 = 0
The solutions of this quadratic equation are:
x_1,2=(hb^2+mφa^2±√((hb^2+mφa^2 )^2-(b^2-〖m^2 a〗^2 )(b^2 h^2-a^2 φ^2-a^2 b^2 ) ))/(b^2-m^2 a^2 )
After rearranging terms, we get the solution:
x_1,2=(hb^2+mφa^2±ab√(2hmφ+φ^2+m^2 h^2+b^2-a^2 m^2 ))/(b^2-m^2 a^2 )
Substituting given values including the slope m = −2 we get:
x_1,2=(2∙6^2-2∙10∙2^2±2∙6√(2∙2∙(-2)10+10^2+(-2)^2 2^2+6^2-2^2 (-2)^2 ))/(6^2-(-2)^2 2^2 )
x_1,2=(-8±12√(-80+100+16+36-16))/(6^2-16)=(-8±89.8)/20=4.09,-4.89
And the  y  coordinates are: y1,2 = −2 x1,2 + 6 = -2.18 , 15.78
The intersection coordinates are:       (4.09 , −2.18)   (−4.89 , 15.78)
NOTES
(1) Notice that pressing on the sign in the equation of the hyperbola or entering a negative number changes the + / − sign and changes the input to positive value.
(2) Calculations are performed during each input digit therefore the hyperbola orientation can be changed. Complete all the inputs to get the desired solution.