☖ Home ⇄ Units Converter ⧉ Geometry Σ Math ✈ Physics 〶 Electricity

Triangle Defined by 3 Points

X1 Y1
X2 Y2
X3 Y3
     
   
Area
Perimeter
Intersection point (x,y) of the medians:
Intersection point (x,y) of the altitudes:
Incircle radius:
Circumcircle radius:
intersection point of the angles bisector (incircle center)
intersection point of the sides perpendicular bisectors (circumcircle center):
Side 1 - 2 Side 1 - 3 Side 2 - 3
Angle   α Angle   β Angle   γ
Altitude h1 Altitude h2 Altitude h3
Median m1 Median m2 Median m3
Intersection of medians
Intersection triangle altitudes (orthocentre)
Intersection perpendicular sides bisectors (circumcircle)
Intersection of the angles bisectors (incircle)

Equations of a triangle defined by 3 points (x1 , y1), (x2 , y2) and (x3 , y3)

Print triangle defined by 3 points
Triangle given by 3 points
(x1 , y1), (x2 , y2) and (x3 , y3)
Triangle definition
The area (A) is given by:
A=1/2 |■(x_1&y_1&1@x_2&y_2&1@x_3&y_3&1)|=1/2 |■(1&1&1@x_1&x_2&x_3@y_1&y_2&y_3 )|
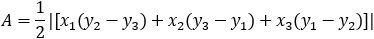Triangle area
The perimeter (P) is:
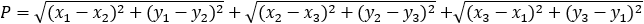Triangle perimeter
Triangle angles:
Triangle angles

If the angle is bigger then 180 degree, then we must translate the angle by the formula:     angle = 2 · π   angle.

Intersection of the medians
Triangle definition 		Intersection point of the medians (x , y)
(centroid - also known as the center of gravity).

Intersection of medians

The lengths of the medians are:

Intersection of medians

Intersection point of the triangle altitudes (orthocentre)

Triangle definition
Intersection of altitudes

After solving the determinants, x and y will be:

x=(y_1 (x_3 x_1+〖y_2〗^2-x_1 x_2-〖y_3〗^2 )-(x_2 x_3+〖y_1〗^2 )(y_2-y_3 )+y_2 (x_1 x_2+〖y_3〗^2 )-y_3 (x_3 x_1+〖y_2〗^2 ))/(x_1 (y_2-y_3 )-y_1 (x_2-x_3 )+x_2 y_3-x_3 y_2 )
y=((〖x_1〗^2+y_2 y_3 )(x_2-x_3 )-x_1 (〖x_2〗^2+y_3 y_1 )+x_1 (〖x_3〗^2+y_1 y_2 )+x_3 (〖x_2〗^2+y_3 y_1 )-x_2 (〖x_3〗^2+y_1 y_2 ))/(x_1 (y_2-y_3 )-y_1 (x_2-x_3 )+x_2 y_3-x_3 y_2 )

The lengths of the altitudes are found by the formulas:

y coordinate of the triangle altitudes intersection

Intersection point of the sides perpendicular bisectors (circumcircle)

Triangle definition
sides perpendicular bisectors intersection

After solving the determinants, we get the x and y coordinates:

x coordinate of sides perpendicular bisectors intersection
y coordinate of sides perpendicular bisectors intersection

The circumcircle radius can be found by calculating the distance of the center point (x , y) from any one of the
triangle vertices:

Incircle radius

Intersection point (x , y) of the angles bisectors (incircle)

Triangle angle bisector definition

We denote a, b and c as the lengths of the triangle sides.

Angles bisectors coordinate

The incircle center x and y is equal to:

Angles bisectors coordinate

The incircle radius can be found by calculating the distance of the center point (x , y) from one of the sides of the triangle:

Incircle radius