☖ Home ⇄ Units Converter ⧉ Geometry Σ Math ✈ Physics 〶 Electricity

Distance of a point to 3D line calculator

Print distance between two 3D lines
Parametric line equation L1
x
 = 
 + t 
y
 = 
 + t 
z
 = 
 + t 
General line equation L1
 x
+
=
 y
+
=
 z
+
Lines defined
by 2 points		 L1
x1
 
   y1
 
   z1
 
x2
 
   y2
 
   z2
 
Distance from point
xp
 
   yp
 
   zp
 
Distance of the point to the line:
 
Connecting point coordinate:
 
Values of  t:
 
       
Distance of 3D line from a point
Presentation of 3D lines
Distance between two 3D lines
Example 1
Example 2
Example 3
Example 4

Calculating distance between two points

Print distance point to 3D line
Two 3d points

The distance between two 3D points is:

d=√((x_2-x_1 )^2+(y_2-y_1 )^2+(z_2-z_1 )^2 )

If point P1 is at the origin then the distance of the point to the origin is:

d=√(〖x_2〗^2+〖y_2〗^2+〖z_2〗^2 )

Calculating distance of a point to a 3D line

Print distance point to 3D line
General axis

The line is given by two points (x1, y1, z1) and (x2, y2, z2)

In parametric notation it can be written as:

L1 = r1 + t e1 = (x1, y1, z1) + t (x2 − x1, y2 − y1, z2 − z1)

The vector   e1 = (x2 − x1)i, (y2 − y1)j, (z2 − z1)k

The vector from point r1 to point P is:

PQ = (px − x1)i + (py − y1)j + (pz − z1)k

The cross product of the line direction vector  e1  with  PQ   PQ ✕ e1  will give us the vector n which is perpendicular to the plane containing both the line and the vector  PQ, it also contains the line that contain the required distance.

Finally, the distance of the point from the line can be calculated by dividing the norm of n by the norm (denoted by double lines) of e1.

d=‖n‖/‖e_1 ‖ =‖PQ×e_1 ‖/‖e_1 ‖

3D lines - Example 1

Print Example 1
Question:
Find the distance between the line L1 = (5, 1, 2) + t(−3, 2, −5) and the
point P(1, 5, −5).
Solution:

From the line equation we denote  r1 = (5, 1, 2)  and  e1 = (−3, 2, −5).

The vector from point r1 to point P is:

QP = (px − x1)i + (py − y1)j + (pz − z1)k

QP = (1 − 5)i + (5 −1)j + (−5 − 2)k = −4i + 4j − 7k

The perpendicular vector to QP and the line is the cross product of this vectors and is:

QP×e_1=|■(i&j&k@-5&1&1@2&4&-9)|=-13i-43j-22k

The norm (magnitude) of the cross product is:

‖QP×e_1 ‖=√(13^2+43^2+22^2 )=√2502=50.02

The norm of the line directions numbers vector is:

‖e_1 ‖=√(2^2+4^2+9^2 )=√101=10.05

And the distance of the line from the point is:

d=‖n‖/‖e_1 ‖ =‖PQ×e_1 ‖/‖e_1 ‖ =50.02/10.05=4.98

3D lines - Example 2

Print Example 2
Question:

Find the distance and the intersection point of the shortest line given by the cartesian form

L_1: (x-3)/2=(y+4)/1=(z-2)/4
and the point P(4, 1, −5).
Solution:

From the line equation we denote  r1 = (3, −4, 2)  and  e1 = (2, 1, 4).

The vector from point r1 to point P is:

QP = (px − x1)i + (py − y1)j + (pz − z1)k

QP = (4 − 3)i + [1 − (−4)]j + (−5 −2)k = i + 5j −7k

The perpendicular vector to QP and the line is the cross product of this vectors and is:

QP×e_1=|■(i&j&k@5&0&-8@2&1&4)|=8i-36j+5k

The norm (magnitude) of the cross product is:

‖QP×e_1 ‖=√(8^2+36^2+5^2 )=√1385=37.22

The norm of the line directions numbers vector is:

‖e_1 ‖=√(2^2+1^2+4^2 )=√21=4.58

And the distance of the line from the point is:

d=‖n‖/‖e_1 ‖ =‖PQ×e_1 ‖/‖e_1 ‖ =37.22/4.58=8.13
A point on the plane
We mark the point (x, y, z) as the intersection point of the shortest line from the given point to the given line. this line is located on the perpendicular plane from line L1. The point P is also located on the same plane and has direction numbers of (2, 1, 4). The following relation is true.
(■(2@1@4))∙(■(x@y@z))=(■(2@1@4))∙(■(4@2@-1))
2x+y+4z=6

To find the shortest line intersection point with the given line, we set the line equation divisions equal to t.

(x-1)/2=(y+2)/1=(z-3)/4=t

We get a set of 3 equations in the x, y and z direction with the unknown t:

x = 2t + 3
y = t − 4
z = 4t + 2

Substitute the values of x, y and z into the equation found before, we get:

2(2t+3)+t-4+4(4t+2)=-11

And the value of the parameter t is:
t=(-21)/21=-1

The value of the intersection point x,y and z is:     (1, −5, −2)

3D lines - Example 3

Print Example 3
Question:

A line is given by two points, (2 , 0 , −1) and (−4 , 2 , 3) Find the distance and the intersection point of the shortest line from point (1 , −3 , 6).

Solution:

The direction numbers of the line considering the two points on the line is:

e = [−4 − 2 , 2 − 0 , 3 − (−1)] = (−6 , 2 , 4)

The line in parametric form is written as:

L: x =   2 − 6t    y = 2t    z = −1 + 4t.

Next, chose an arbitrary point on the line, by letting  t = 0  or any other value for  t, the point on the line will be:   (2 , 0 , −1)

The vector connecting the given point with the point on the line is  PQ.

PQ = (1 − 2 , −3 − 0 , 6 + 1) = (−1, −3 , 7)

The perpendicular vector to line PQ and the given line is the cross product:

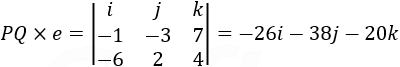
PQ×e=|■(i&j&k@-1&-3&7@-6&2&4)|=-26i-38j-20k

The length of this vector is the modulus:

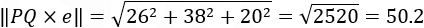
‖PQ×e‖=√(26^2+38^2+20^2 )=√2520=50.2

The modulus of the direction numbers is:

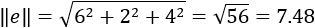
‖e‖=√(6^2+2^2+4^2 )=√56=7.48

And the length of the shortest line between the point and the given line is:

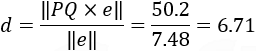
d=‖PQ×e‖/‖e‖ =50.2/7.48=6.71

To find the intersection point, we use the fact that vector PQ' should be perpendicular to the line, hence the dot product of the direction numbers of the line e and the vector PQ defined with the value t, results is 0.

PQ' = (2 − 6t − 1 , 2t +3 , −1 + 4t − 6 = (1 − 6t , 3 + 2t , 4t − 7)

PQ' . e = (1 − 6t , 3 + 2t , 4t − 7) • (− 6 , 2 , 4) = −6 + 36t + 6 + 4t 16t = 0

56 t − 28 = 0       -> t = 0.5

And the intersection point is:

(x = 2 − 4 ∙ 0.5    y = 2 ∙ 0.5    z = −1 + 4 ∙ 0.5) = (−1, 1 , 1)

Detail solution of distance of a point to 3D line - Example 4

Print Example 4
Question:

Find the distance of the point P(2 , 5 , 1) from the line

(x+3)/(-4)=(y-2)/5=(z+4)/(-2)

Solution:

For solution we will use the cross and dot product of vectors.

In parametric form the line is:  L:  x = −3 − 4t ,   y = 2 + 2t ,   z = −4 − 2t

The coefficients of t are the direction numbers  e  (or the vector) describing the line direction:   e = (−4 , 2 , −2).

Drawing of example 4

Now we shall find an arbitrary point (x, y, z) on the line, it can be done for example by choosing t = 0 or any other value in the parametric line:

We get (x, y, z) = (−3 , 2 , −4)

Now we can find the value of the vector PQ.

PQ = [2 − (− 3) , 5 − 2 , 1 − (−4)] = (5 , 3 , 5)

The cross product of PQ and e will give a vector who is perpendicular to the plan containing PQ and the line, we mark this vector by  n:

n=PQ×e=|■(i&j&k@5&3&5@-4&2&-2)|=-16i-10j+22k

Now if we cross multiply the vector n with the line vector (direction numbers) we will get a vector perpendicular to the line, this vector is in the direction of the shortest line from the point to the line.

m=n×e=|■(i&j&k@-1&-10&-23@-4&5&-2)|=135i+90j-45k

Next, we find the unit vector in the m direction.

m ̂=m/‖m‖ =(135i+90j-45k)/√(135^2+90^2+45^2 )=0.8i+0.53j-0.267k

Now the only step remained to find the shortest line length is to project vector PQ on the unit vector in the direction of the shortest line, this is done by dot product of PQ with the unit vector.

d=PQ∙m ̂=(5i ,3j ,5k)∙(-0.17i-0.85j-0.51k)=5.95

If we want to find the shortest line intersection point with the given line, we find the value of PQ as a function of  t.

PQ = (−3 −4t − 2 , 2 + 2t − 5 , −4 −2t − 1) = (−5 −4t , −3 + 2t , −5 −2t)

Now we use the fact that if the dot product of two vectors is 0 then the vectors are perpendicular to each other.

PQ ‧ e = (−5 −4t , −3 + 2t , −5 −2t) ‧ (−4 , 2 , −2) = 0

PQ ‧ e = (20 + 16t −6 + 4t + 10 + 4t) = 0

24 + 24t = 0
→
t = −1

And the intersection point, after substituting the value of t into the parametric equation of the line is:

(x,y,z) = [−3 −4 * (−1) , 2 + 2 * (−1) , −4 −2 * (−1)] = (1 , 0 , −2)