☖ Home ⇄ Units Converter ⧉ Geometry Σ Math ✈ Physics 〶 Electricity

Circle defined by 3 points calculator

Print circle 3 points
X1 
Y1 
X2 
Y2 
X3 
Y3 
Center point (x,y):
Radius:
Area of circle:
Perimeter of circle:
Circle equation:
r2
                         
Circle 3 points summary
Example 1
Example 2
Example 3

Equation of a circle passing through 3 points (x1, y1) (x2, y2) and (x3, y3) summary

Print 3 points circle summary
The equation of the circle is described by the equation:

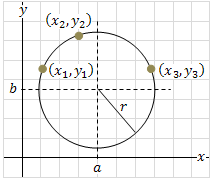
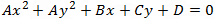
Circle equation

After substituting the three given points which lies on the circle, we get the set of equations that can be described by the determinant:

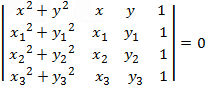
Circle equation
The coefficients A, B, C and D can be found by solving the following determinants:
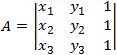
Circle equation A
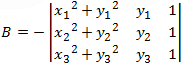
Circle equation B
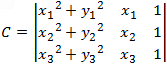
Circle equation C
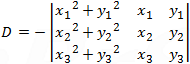
Circle equation D
Circle equation

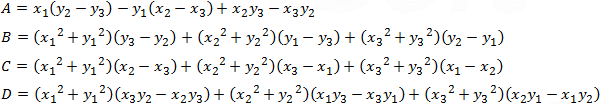
Center point  (x, y)  and the radius of a circle passing through 3 points  (x1, y1) (x2, y2)  and  (x3, y3)  are:

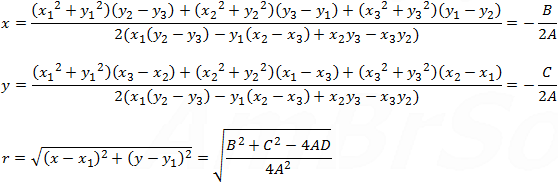
Circle equation

Example 1 - Circle Defined by 3 Points

Ex-1
Find the equation of a circle that passes through the points (⎯3 , 4) , (4 , 5) and (1 , ⎯4).
Using the equations for  A , B , C  and  D  developed before we have:
A = ⎯ 3(5 ⧾ 4) ⎯ 4(4 ⎯ 1) ⧾ 4(⎯4) ⎯ 1 • 5 = −60

B = (9 ⧾ 16)(⎯4 ⎯ 5) ⧾ (16 ⧾ 25)(4 ⧾ 4) ⧾ (1 ⧾ 16)(5 ⎯ 4) = 120

C = (9 ⧾ 16)(4 ⎯ 1) ⧾ (16 ⧾ 25)(1 ⧾ 3) ⧾ (1 ⧾ 16)(⎯3 ⎯ 4) = 120

D = (9 ⧾ 16)[1 • 5 ⎯ 4(⎯4)] ⧾ (16 ⧾ 25)[⎯3 • (⎯4) ⎯ 1 · 4] ⧾ (1 ⧾ 16)[4 • 4 ⎯ (⎯3) 5] = 1380

Divide all terms by  ⎯60  to obtain:
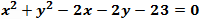
(x-1)^2+(y-1)^2=25

To find the equation of the circle represented by standard form we can use the equations described in the summary or use the complementary square method as described bellow:

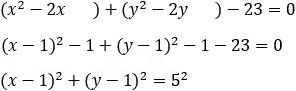
(x^2-2x )+(y^2-2y )-23=0 (x-1)^2-1+(y-1)^2-1-23=0 (x-1)^2+(y-1)^2=5^2

The center of the circle is oviouse and is  x = 1  and  y = 1 (1, 1)

And the radius of the circle is:   5

Another way to find the circle's equation is by substituting the points into the circle general equation, each of theme should satisfy the equation of the circle.

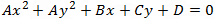
Circle equation
We will asume that A = 1
Point (−3 , 4)
9 + 16 −3B + 4C + D = 0
→
−3B + 4C + D = −25
Point (4 , 5)
16 + 25 −4B + 5C + D = 0
→
4B + 5C + D = −41
Point (1 , −4)
1 + 16 + B −4C + D = 0
→
B − 4C + D = −17

We got 3 equations with 3 unknowns B, C and D, solving thos equations we shell get the same solution.

Example 2 - Circle Defined by 3 Points

Ex-2
Find the equation of a circle and its center and radius if the circle passes through the points (3 , 2) ,
(6 , 3) and (0 , 3).
The general equation of a circle is given by the equation:
Ax2 + Ay2 + Bx + Cy + D = 0

Because each point given should fulfill the equation of the circle we have to solve the following set of equations with the unknowns A, B, C and D:

A(x2 + y2) + Bx + Cy + D = 0
A(x12 + y12) + Bx1 + Cy1 + D = 0
A(x22 + y22) + Bx2 + Cy2 + D = 0
A(x32 + y32) + Bx3 + Cy3 + D = 0
or
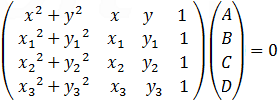
(█(■(x^2+y^2&x&y 1@〖x_1〗^2+〖y_1〗^2&x_1&y_1 1@〖x_2〗^2+〖y_2〗^2&x_2&y_2 1)@ 〖x_3〗^2+〖y_3〗^2 x_3 y_3 1 ))(■(A@B@■(C@D)))=0

Because all the equations equal to 0 also the determinant of the coefficients should be equal to 0 and the value of the determinant will be as follows:

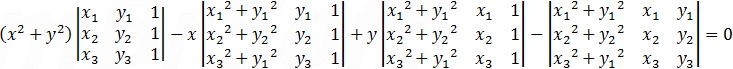
(x^2+y^2 )|■(x_1&y_1&1@x_2&y_2&1@x_3&y_3&1)|-x|■(〖x_1〗^2+〖y_1〗^2&y_1&1@〖x_2〗^2+〖y_2〗^2&y_2&1@〖x_3〗^2+〖y_1〗^2&y_3&1)|+y|■(〖x_1〗^2+〖y_1〗^2&x_1&1@〖x_2〗^2+〖y_2〗^2&x_2&1@〖x_3〗^2+〖y_1〗^2&x_3&1)|-|■(〖x_1〗^2+〖y_1〗^2&x_1&y_1@〖x_2〗^2+〖y_2〗^2&x_2&y_2@〖x_3〗^2+〖y_1〗^2&x_3&y_3 )|

Notice that we got the equation of a circle with the determinants equal to the coefficients  A, B, C and D as follows;       (x2 + y2)A + xB + yC + D = 0.

A=|■(3&2&1@6&3&1@0&3&1)|=6
B=|■(13&2&1@45&3&1@9&3&1)|=36
C=|■(13&3&1@45&6&1@9&0&1)|=-84
D=|■(13&3&2@45&6&3@9&0&3)|=-198

After dividing all terms by 6 we get:    A = 1    B =−6    C = −14    D = 33.

And the equation of the circle is:    x2 + y2 ⎯ 6x ⎯ 14y + 33 = 0

In order to find the radius of the circle use the general circle equation and perform some basic algebraic steps and with the help of the square form   (a + b)2 = a2 + 2ab + b2   we get

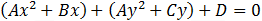
(Ax^2+Bx)+(Ay^2+Cy)+D=0

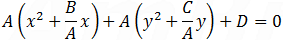
A(x^2+B/A x)+A(y^2+C/A y)+D=0

A[(x+B/2A)^2-B^2/(4A^2 )]+A[(y+C/2A)^2-C^2/(4A^2 )]+D=0

[(x+B/2A)^2-B^2/(4A^2 )]+[(y+C/2A)^2-C^2/(4A^2 )]=-D/A

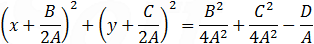
(x+B/2A)^2+(y+C/2A)^2=B^2/(4A^2 )+C^2/(4A^2 )-D/A

The last equation is a circle with the center and radius equals to (notice the minus sign at x and y):

x=-B/2A
and
y=-C/2A
and the radius is:
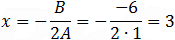
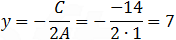
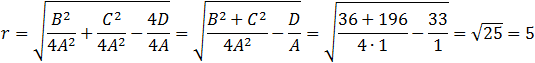
r=√(B^2/(4A^2 )+C^2/(4A^2 )-4D/4A)=√((B^2+C^2)/(4A^2 )-D/A)

The equation of the circle can be presented by the center and the radius as:     (x ⎯ 3)2 + (y ⎯ 7)2 = 52

Example 3 - Circle Defined by 2 Points and the y axis

Ex-3
Find the equation of a circle that has its center on the y axis and passes through the points (−2 , 3) , and (4 , 1).

We have to find a circle that the center is on the y axis, so the circle equation should look like:

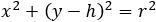
x^2+(y-h)^2=r^2

And after opening the parenthesis:
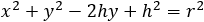
x^2+y^2-2hy+h^2=r^2

Now we can substitute both points into the circle equation:

point (4 , 1)
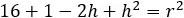
16+1-2h+h^2=r^2
point (−2 , 3)
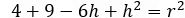
4+9-6h+h^2=r^2
Subtract lower equation from the upper:
4+4h=0 → h=-1

To find the radius of the circle we substitute the value h = −1 into the circle equation:

17 + 2 + 1 = r2   and   r2 = 20

Hence the circle equation will be:
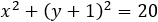
x^2+(y+1)^2=20

The location of all circle center families can be defined as follows:

k h Center location
k = 0 h = 0 Origin
k = 0 h ≠ 0 On y axis
k ≠ 0 h = 0 On x axis
k ≠ 0 h = k On line 45°
k ≠ 0 h ≠ 0 Anywhere